Generadores pseudo-aleatorios

Todos los lenguajes de programación (o casi todos) tienen un generador pseudo-aleatorio. Las sintaxis varían: ran, grand, rand, Random... Estas son funciones que, según los manuales de usuarios, ``dan como resultado números al azar''. Lo que se entiende por ``números al azar'' depende, en principio, del tipo de número (booleanos, enteros, reales). Convenimos en denotar por Random a la función que ``da como resultado un número real al azar en el intervalo

''. Esta frase contiene, de hecho, a dos propiedades distintas, que admitiremos como postulados.

En el lenguaje corriente ``al azar'' no significa solamente aleatorio si no también uniformemente distribuido. Seleccionar al azar, es dar las mismas oportunidades a todos los resultados posibles (equiprobabilidad). Lo que se espera de un número real seleccionado ``al azar'' en

es que caiga entre

con probabilidad

, y esta probabilidad es la misma de caer entre

. Dos intervalos incluidos en

tienen la misma probabilidad de que el número se encuentre en ellos, si tienen la misma longitud, y esta probabilidad es la longitud de los intervalos. Los postulados anteriores tienen otra consecuencia. Si se consideran pares sucesivos de llamadas de la función Random como las coordenadas de un punto en el plano, estos puntos son ``puntos al azar'' en

(ver la figura 1). El significado preciso es que estos puntos son independientes y además:

La probabilidad de que un punto, cuyas coordenadas son obtenidas a partir de la función Random, caiga en un cierto rectángulo es igual a la superficie del rectángulo. Esto puede, evidentemente, extenderse a cualquier dimensión. Tríos de llamadas sucesivas de Random, son las coordenadas de ``puntos al azar'' en el cubo

, etc...

Proposición 2.1 Para todo $k\in\mathbb {N}^*$ , sean $(R_1,\ldots ,R_k)$

llamadas consecutivas de Random. Los postulados 1) y 2) implican que para todo rectángulo

$\displaystyle D= ]a_1,b_1]\times\cdots\times]a_k,b_k],$ donde $\displaystyle 0\leq a_i<b_i\leq 1~, \forall i=1,\ldots ,k~,$

se tiene:

$\displaystyle \mathbb {P}[~(R_1,\ldots ,R_k)\in D~] =(b_1-a_1)\cdots (b_k-a_k) \;.$

$\displaystyle \forall \varepsilon >0\,,\; \mathbb {P}[~$ Random $\displaystyle =a~] \leq \mathbb {P}[~$ Random $\displaystyle \in ]a-\varepsilon,~a]~] =\varepsilon \;.$

$\displaystyle \mathbb {P}[~$ `Random` $\displaystyle \in~ ]a,b]~]$	$\displaystyle =$	$\displaystyle \mathbb {P}[~$ `Random` $\displaystyle \in [a,b]~]$
	$\displaystyle =$	$\displaystyle \mathbb {P}[~$ `Random` $\displaystyle \in [a,b[~]$
	$\displaystyle =$	$\displaystyle \mathbb {P}[~$ `Random` $\displaystyle \in ]a,b[~] \;.$

Al admitir a la vez que Random puede tomar un número infinito de valores diferentes y que la probabilidad de tomar un valor especifico es nula, tenemos una paradoja. Veremos en situaciones prácticas que la situación es ligeramente diferente, sin que por ello nos cuestionemos los postulados de la definición de Random. Una vez aceptados los dos postulados, todo análisis de algoritmo que contiene a Random, es una demostración matemática tan rigurosa como otra.

$\displaystyle \mathbb {P}[D=k]$	$\displaystyle =$	$\displaystyle \mathbb {P}[$ Int( `Random` $\displaystyle * 6)=k-1~]$
	$\displaystyle =$	$\displaystyle \mathbb {P}[\,$ `Random` $\displaystyle * 6\in [k-1,k[~]$
	$\displaystyle =$	$\displaystyle \mathbb {P}[$ `Random` $\displaystyle \in [(k-1)/6, ~k/6[ ~]$
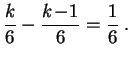	$\displaystyle =$	$\displaystyle \frac{k}{6}-\frac{k\!-\!1}{6}=\frac{1}{6}\;.$

No hay que deducir de este ejemplo que Int

Random

es la mejor forma de obtener un entero al azar entre 0 y $k\!-\!1$ . Los generadores de números aleatorios usuales permiten tener tipos diferentes de números como resultado: números reales distribuidos uniformemente en el intervalo

, booleanos, enteros y aún complejos.

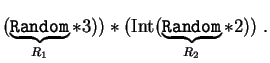
$\displaystyle X\longleftarrow ($ Int $\displaystyle ( \underbrace {\mbox{\tt Random} }_{R_1} * 3))* (\mbox{Int}( \underbrace {\mbox{\tt Random}}_{R_2}* 2))\;.$

$\displaystyle \mathbb {P}[X=2]$	$\displaystyle =$	$\displaystyle \mathbb {P}[$ Int $\displaystyle (R_1* 3)=2$ y Int $\displaystyle (R_2* 2)=1~]$
	$\displaystyle =$	$\displaystyle \mathbb {P}[~R_1\in [2/3,~1[$ y $\displaystyle R_2\in[1/2,~1[~]$
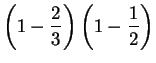	$\displaystyle =$	$\displaystyle \left(1-\frac{2}{3}\right)\left(1-\frac{1}{2}\right)$
	$\displaystyle =$	$\displaystyle \frac{1}{6}\;.$

Observación: Contrario a las apariencias, el algoritmo anterior no da valores entre

. Teóricamente, la probabilidad de que Random dé el valor

es nula. En la práctica, los generadores están, en general, hechos de manera tal que nunca dan ni 0 ni

Los generadores aleatorios permiten simular sucesiones de experimentos aleatorios independientes y por tanto podemos calcular, de forma aproximada, probabilidades aplicando la Ley de los Grandes Números. El algoritmo genérico de cálculo de una frecuencia experimental tomará la siguiente forma.