Vamos a dar tres ejemplos de experimentos aleatorios que nos
permitirán discernir el papel que desempeñan las matemáticas y la
simulación, respectivamente, en la modelación de experimentos
aleatorios.
Ejemplo 1 : Aguja de Buffon.
Se lanza al azar una aguja sobre un
parqué. Se supone, para simplificar, que la longitud de la aguja
es igual al ancho de una de las tablillas del parqué. El problema
consiste en calcular la probabilidad de que la aguja caiga entre
![]() de las tablillas.
de las tablillas.
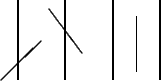
Una concretización de este experimento se encuentra en el
``Palacio de los Descubrimientos'' en París : las
``tablillas del parqué'' son metálicas, la aguja está agarrada por
un electroimán y cae cuando un visitante oprime un interruptor. Si
cae entre dos láminas de metal, se cierra un circuito y un
contador se incrementa. Podemos consecuentemente calcular la
frecuencia experimental. Esta se encuentra muy cerca
de ![]() (millones de visitantes han hecho funcionar el
interruptor ...). Por tanto tenemos una forma ``experimental''
de calcular
(millones de visitantes han hecho funcionar el
interruptor ...). Por tanto tenemos una forma ``experimental''
de calcular ![]() . Notemos que el experimento del Palacio de los
Descubrimientos es ya una analogía, una idealización del problema
inicial: es un modelo físico.
. Notemos que el experimento del Palacio de los
Descubrimientos es ya una analogía, una idealización del problema
inicial: es un modelo físico.
Modelo matemático.
Las hipótesis son las siguientes.
Cálculo por simulación :
Aproximamos la probabilidad buscada por
una frecuencia empírica, calculada empleando el siguiente
algoritmo.
![]()
Repetir ![]() veces
veces
![]() Random
Random![]()
![]() Random
Random ![]()
Si
![]() Entonces
Entonces
![]()
finSi
finRepetir
frecuencia
![]() .
.
Veamos como ejemplo una
frecuencia obtenida a partir de ![]() experimentos.
experimentos.
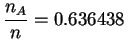 o sea
o sea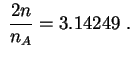
En ambos casos (cálculo matemático y
simulación) no hemos hecho más que desarrollar las consecuencias
de las hipótesis de definición del modelo. La simulación no tiene
una mayor relación con la realidad física que el cálculo
matemático. De hecho, estamos obligados a introducir el valor de
![]() en el algoritmo, para en fin de cuentas... deducir una
estimación de este valor! El milagro es que las consecuencias
calculadas a partir de las hipótesis de modelación, puedan tener
una relación con una realidad física, o dicho en otras palabras,
que el modelo matemático pueda ser validado al confrontarlo
con el experimento.
en el algoritmo, para en fin de cuentas... deducir una
estimación de este valor! El milagro es que las consecuencias
calculadas a partir de las hipótesis de modelación, puedan tener
una relación con una realidad física, o dicho en otras palabras,
que el modelo matemático pueda ser validado al confrontarlo
con el experimento.
Ejemplo 2 : Paradoja de Bertrand.
En un círculo de radio ![]() , ¿cuál es
la probabilidad para que una cuerda seleccionada al azar sea
de longitud superior a
, ¿cuál es
la probabilidad para que una cuerda seleccionada al azar sea
de longitud superior a ![]() ?
? ![]() es la longitud del
lado del triángulo equilátero inscrito en el círculo.
es la longitud del
lado del triángulo equilátero inscrito en el círculo.
Modelo 1
En el disco se selecciona al azar un
punto y se le asocia la cuerda de la cual él es el punto medio. El
evento se realiza si el punto se encuentra en el disco concéntrico
de radio ![]() :
:
Modelo 2 Se selecciona el punto medio de la
cuerda sacando al azar sus coordenadas polares: ![]() un número
real al azar entre 0 y
un número
real al azar entre 0 y ![]() ,
, ![]() un número real al azar
entre 0 y
un número real al azar
entre 0 y ![]() . El evento se realiza si
. El evento se realiza si
![]() :
:
Modelo 3 Se seleccionan los dos extremos de la cuerda al azar en la circunferencia:
No debe ser chocante el hecho que hipótesis de modelación
diferentes conduzcan a conclusiones diferentes. Se podría simular
cada uno de los modelos propuestos y deducir las diferentes
probabilidades anunciadas por el razonamiento. No podemos decir
que un modelo es más ``verdadero'' que los otros mientras no
exista un experimento físico para validar los resultados.
Ejemplo 3: Un truco con cartas.
Se asigna un valor a cada carta de un juego de ![]() cartas: los
ases valen
cartas: los
ases valen ![]() , los ``
, los ``![]() '' valen
'' valen ![]() , y así sucesivamente hasta
los ``
, y así sucesivamente hasta
los ``![]() ''. Las sotas, reinas y reyes valen
''. Las sotas, reinas y reyes valen ![]() . Las cartas se
extienden en una fila después de haberlas barajado.
. Las cartas se
extienden en una fila después de haberlas barajado.
Se selecciona una carta entre las ![]() primeras y se avanza hacia
la derecha tantas cartas como indica el valor de la carta
seleccionada. Se llega así a una carta que indica nuevamente
cuantas cartas hay que avanzar hacia la derecha en el próximo
paso. Se repite el proceso hasta que no se puede avanzar más (por
ejemplo la carta que se levanta es un
primeras y se avanza hacia
la derecha tantas cartas como indica el valor de la carta
seleccionada. Se llega así a una carta que indica nuevamente
cuantas cartas hay que avanzar hacia la derecha en el próximo
paso. Se repite el proceso hasta que no se puede avanzar más (por
ejemplo la carta que se levanta es un ![]() y solamente quedan
y solamente quedan ![]() cartas a la derecha). La última carta que se levanta es la carta
final. El mago se propone adivinar cual es la carta final, sin
saber nada sobre el recorrido. Para esto él selecciona también una
carta entre las 9 primeras e itera el mismo algoritmo. Él anuncia
que vuestra carta final es la misma que la suya.
cartas a la derecha). La última carta que se levanta es la carta
final. El mago se propone adivinar cual es la carta final, sin
saber nada sobre el recorrido. Para esto él selecciona también una
carta entre las 9 primeras e itera el mismo algoritmo. Él anuncia
que vuestra carta final es la misma que la suya.
Si las cartas se barajaron al azar, ¿qué probabilidad tiene el
mago de adivinar correctamente? Yo no conozco una respuesta
matemática a esta pregunta. Si existe una, es seguramente
complicada (el número de permutaciones de ![]() cartas,
cartas, ![]() tiene
tiene
![]() cifras).
cifras).
Cuando un modelo es demasiado complicado para ser tratado
matemáticamente se impone recurrir a la simulación. Presentamos
una
frecuencia experimental obtenida a partir de la simulación de
![]() permutaciones aleatorias de las
permutaciones aleatorias de las ![]() cartas:
cartas: