Sección : Simulación, modelos y realidad
Previo : Generadores pseudo-aleatorios
Siguiente : Complejidad y aleatoriedad

Sucesiones uniformes

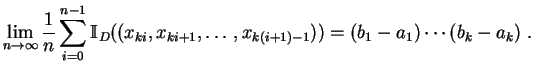
Al observar una sucesión de números reales, dada por un generador aleatorio específico, ¿cómo decidir si este generador es adecuado? La única forma práctica de estimar una probabilidad es expresarla como un límite de frecuencias experimentales.

Definición 2.2   Una sucesión $(x_n),$ $n\in\mathbb {N}$, con valores en $[0,1]$, se dice que es $k$-uniforme si para todo rectángulo

$$D= ]a_1,b_1]\times\cdots\times]a_k,b_k],$$    donde $$0\leq a_i<b_i\leq 1~, \forall i=1,\ldots ,k~,$$

se tiene:

$$\lim_{n\rightarrow \infty}\frac{1}{n} \sum\limits^{n-1}_{i=0} \... ..._D((x_{ki}, x_{ki+1},\ldots , x_{k(i+1)-1})) =(b_1-a_1)\cdots (b_k-a_k) \;.$$

$\mathbb {I}_D$ denota la función indicatriz del conjunto $D$ :

$$\mathbb {I}_D(y) = \left\{ \begin{array}{cl} 1 &\mbox{ si } y\in D\,,\\ 0 &\mbox{ si no }. \end{array}\right.$$

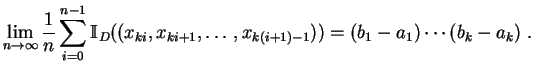
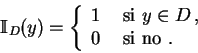
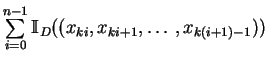El vector $(x_{ki}, x_{ki+1},\ldots , x_{k(i+1)-1})$ es la $i$-ésima $k$-tupla de elementos consecutivos de la sucesión. la suma $\sum\limits^{n-1}_{i=0}\mathbb {I} _D((x_{ki}, x_{ki+1},\ldots , x_{k(i+1)-1}))$ es el número de $k$-tuplas de elementos consecutivos de la sucesión que están en $D$, entre los $n$ primeros.

Por tanto, la definición anterior dice que entre las $k$-tuplas de elementos consecutivos de elementos de la sucesión, la proporción de los que caen en un rectángulo dado debe tender al volumen de ese rectángulo (en dimensión $k$). Esta definición es pasablemente utópica. En particular ella conlleva a que la probabilidad de que Random caiga en un punto prefijado es nula. Sabiendo que sólo hay una cantidad numerable de números racionales en $[0,1]$, la probabilidad de caer sobre un número racional es de también nula. Pero la computadora conoce solamente los números decimales, y aún más un número finito de ellos, por tanto la función Random no puede dar como resultado otra cosa que números racionales. Pero esto no es un inconveniente. Si sabemos construir una sucesión uniforme de dígitos entre 0 y $9$, podremos obtener números reales al azar en $[0,1]$, aproximados hasta la $k$-ésima posición decimal, considerando $k$-tuplas consecutivas de dígitos de la sucesión original. Este es el principio de las ``tablas de números aleatorios'' que todavía se encuentran en algunos libros. La misma observación puede hacerse en base $2$. Es suficiente saber definir que cosa es una sucesión aleatoria de bits. Veamos a continuación la definición de $k$-uniformidad para las sucesiones booleanas 0 o $1$).

Definición 2.3   Una sucesión $x=(x_n)$ de números booleanos en $\{0, 1\}$ se dice que es uniforme si para todo $(\varepsilon _1,\ldots ,\varepsilon_k)\in \{0,1\}^k$ :

$$\lim\limits_{n\rightarrow\infty}\frac{1}{n}\sum\limits^{n-1}_{i=0... ...varepsilon_k)\}} ((x_{ki},x_{ki+1},\ldots ,x_{k(i+1)-1}))=\frac{1}{2^k} \;.$$

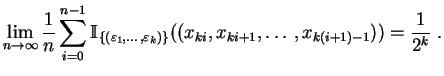
Lo que esperamos de la sucesión de llamadas de Random, es que la sucesión que se obtiene sea $k$-uniforme, para todo entero $k$ (decimos $\infty$-uniforme). Esto es evidentemente ilusorio, porque el infinito no existe en un ordenador. Lo más que podemos hacer es verificar que nada inverosímil se produce en la sucesión finita observada. Precisamente este es el objetivo de los tests estadísticos, separar lo plausible de lo que es poco verosímil. Multitud de tests han sido pensados para probar a los generadores aleatorios.

``Definición'' Una $N$-tupla de números en $[0,1]$ será llamada pseudo aleatoria si pasa con éxito una serie de tests estadísticos, cada uno de ellos con el objetivo de verificar una consecuencia de la $k$-uniformidad. El número de los tests, así como el entero $k$ son una función creciente de la exigencia del usuario.

Entre las diferentes formalizaciones del azar que pudieron haber sido propuestas, la noción de sucesión $\infty$-uniforme es la única utilizable en la práctica: ella es la única que podemos comprobar para un generador dado y ella basta para justificar todas las aplicaciones de los generadores pseudo-aleatorios. Los generadores que se suministran con los compiladores más usados vienen de una larga experimentación estadística, y han sobrevivido a lo largo del tiempo porque satisfacen las necesidades de numerosos usuarios, lo que no impide que se mantengan bajo vigilancia.

¿Cómo están programados? Aún las sucesiones recurrentes más simples pueden ser caóticas y por tanto ser ejemplos de sucesiones aparentemente aleatorias. Y esto, aún el sentido intuitivo de aleatorio (imposible de prever), está en contradicción con la definición de una sucesión por recurrencia (cada término es una función conocida del anterior). Para un ordenador sólo existe un número finito de valores. Los valores de Random son calculados siempre a partir de enteros distribuidos en $\{0,1,\ldots ,M\!-\!1\}$ donde $M$ es un número grande (del orden de $10^8$ al menos para los generadores usuales). Para dar un número real en $[0,1]$, basta dividir por $M$. En la práctica sólo puede obtenerse un número finito de valores, y esto con probabilidad positiva. Esto contradice los postulados de la definición de Random, pero no constituye un inconveniente importante en la medida en que $M$ sea muy grande. Para obtener otro tipo de valores, por ejemplo números enteros distribuidos uniformemente en $\{0,\ldots,k\}$ o números booleanos (cara o cruz), es inútil pasar por llamadas de Random, es mejor partir directamente del generador sobre $\{0,\ldots,M\!-\!1\}$ sin dividir previamente por $M$. Esto se tiene en cuenta en la mayoría de los lenguajes en uso.

El valor que nos da un generador es una función del valor precedente o de varios valores obtenidos con anterioridad. En el primer caso, la sucesión que se calcula es una sucesión recurrente. Para comenzar el proceso se selecciona una ``semilla'', $u_0$, en el conjunto $\{0,\ldots,M\!-\!1\}$, los valores de la sucesión se calculan a partir de una expresión $u_{n+1}=g(u_n)$, donde $g$ es una función de $\{0,\ldots,M\!-\!1\}$ en si mismo, suficientemente simple como para ser calculada rápidamente.

Nos enfrentamos entonces a un problema importante: toda sucesión recurrente sobre un conjunto finito es periódica. La sucesión de valores que nos da Random hará, necesariamente, un lazo. ¿Podemos considerar como aleatoria a una sucesión periódica? Sí, puede ser, si el período es lo suficientemente grande en relación con el número de términos que vamos a emplear. La prudencia debe prevalecer en general, de todas formas hay que evitar la idea intuitiva de que mientras más complicada sea la forma de calcular $u_{n+1}$ a partir de $u_n$, más independientes serán los valores entre síy el generador será mejor. Los generadores aleatorios más simples son los generadores por congruencias. Ellos son de la siguiente forma:

$$g(u)\;=\;(A u+C)\;$$modulo $$M \;.$$

Resultados diversos en matemáticas, dicen cómo seleccionar ``correctamente'' $A$, $C$ y $M$. Ya prácticamente no se usan, desde que aparecieron nuevos generadores mas eficientes. El generador que damos a continuación estaba muy difundido y en general era satisfactorio; todavía puede ser útil.

$$g(u)\;=\;16807 \,u\;$$ modulo $$\,2147483647\;.$$

Todo generador necesita una inicialización. Para un mismo valor de la semilla $u_0$, se obtiene siempre la misma sucesión de valores al emplear el generador. Para obtener resultados diferentes de una sucesión a otra, es necesario cambiar la semilla al principio de cada calculo. En dependencia del lenguaje que se utilice, esta inicialización puede dejarse a la elección del usuario, o puede ser realizada a partir del contador de tiempo del ordenador(función randomize en Pascal, seed en C...). La instrucción de tomar una semilla aleatoria debe figurar una sola vez, al principio del programa principal.

Sección : Simulación, modelos y realidad
Previo : Generadores pseudo-aleatorios
Siguiente : Complejidad y aleatoriedad