La idea de la
estimación
por
intervalo de confianza es definir, alrededor de la
media empírica, un intervalo aleatorio (que depende de ![]() experimentos) que contiene a
experimentos) que contiene a ![]() con una probabilidad alta. La
longitud de este intervalo es la que mide la exactitud de la
estimación.
con una probabilidad alta. La
longitud de este intervalo es la que mide la exactitud de la
estimación.
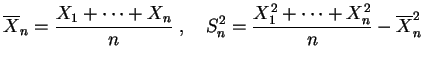 y
y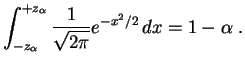
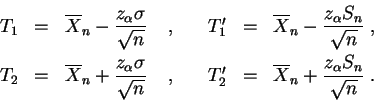
Interpretación:
Como el valor de ![]() es desconocido no hay ninguna razón a
priori para que la
desviación estándar
es desconocido no hay ninguna razón a
priori para que la
desviación estándar ![]() sea conocida. Si
es desconocida, se la estima por la
desviación estándar empírica
sea conocida. Si
es desconocida, se la estima por la
desviación estándar empírica
![]() . Esta es la razón por la cual damos dos
intervalos de
confianza. El valor de
. Esta es la razón por la cual damos dos
intervalos de
confianza. El valor de ![]() se
obtiene a partir de un módulo de cálculo numérico. Los valores más
usados son los siguientes:
se
obtiene a partir de un módulo de cálculo numérico. Los valores más
usados son los siguientes:

Los intervalos ![]() y
y
![]() son aleatorios. Como
resultado de la sucesión de experimentos ,
son aleatorios. Como
resultado de la sucesión de experimentos , ![]() y
y ![]() habrán
tomado valores particulares
habrán
tomado valores particulares ![]() y
y ![]() . No se podrá decir que
la probabilidad de que
. No se podrá decir que
la probabilidad de que ![]() pertenezca a
pertenezca a
![]() es de
es de
![]() . Tanto
. Tanto ![]() como
como ![]() y
y ![]() son números reales
fijos y el resultado
son números reales
fijos y el resultado
![]() será verdadero o falso,
pero no dependerá ya del azar. Lo que podremos decir es que este
encuadre (de
será verdadero o falso,
pero no dependerá ya del azar. Lo que podremos decir es que este
encuadre (de ![]() entre
entre ![]() y
y ![]() ) se obtiene como resultado
de un experimento que tenia un porcentaje alto de posibilidades de
dar un resultado verdadero. Para
) se obtiene como resultado
de un experimento que tenia un porcentaje alto de posibilidades de
dar un resultado verdadero. Para
![]() , si repetimos
, si repetimos
![]() veces la serie de
veces la serie de ![]() experimentos para obtener
experimentos para obtener ![]() intervalos, podemos esperar que uno de ellos sea falso. Hay que ver un intervalo de confianza como una precisión que se da
del valor estimado de
intervalos, podemos esperar que uno de ellos sea falso. Hay que ver un intervalo de confianza como una precisión que se da
del valor estimado de ![]() :
:
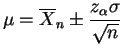 ó
ó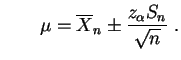
Estimación de una probabilidad.
Supongamos que el valor que hay que estimar sea la probabilidad
![]() de un evento. Se realizan una serie de experimentos
independientes anotando, cada vez, si el evento se realiza (
de un evento. Se realizan una serie de experimentos
independientes anotando, cada vez, si el evento se realiza (![]() ) o
no (0). La variable aleatoria correspondiente a el
) o
no (0). La variable aleatoria correspondiente a el ![]() -ésimo
experimento se denota por
-ésimo
experimento se denota por ![]() . Las
. Las ![]() siguen la
ley de
Bernoulli de parámetro
siguen la
ley de
Bernoulli de parámetro ![]() :
:
Volvamos a la experiencia de la
aguja de Buffon. Esta consiste en lanzar al azar una aguja sobre
un parqué. Si el ancho de las láminas de madera es igual a la
longitud de la aguja, hemos visto que la probabilidad (teórica)
para que la aguja caiga sobre 2 láminas a la vez es ![]() .
Supongamos que repetimos el experimento
.
Supongamos que repetimos el experimento ![]() veces, físicamente o
por simulación. Como resultado de las
veces, físicamente o
por simulación. Como resultado de las ![]() repeticiones obtenemos
un valor para la
frecuencia experimental
repeticiones obtenemos
un valor para la
frecuencia experimental
![]() y por
tanto un intervalo de confianza
y por
tanto un intervalo de confianza ![]() . El intervalo
. El intervalo
![]() es también un
intervalo de confianza para el valor
de
es también un
intervalo de confianza para el valor
de ![]() . He aquí , por ejemplo, un
resultado obtenido con
. He aquí , por ejemplo, un
resultado obtenido con ![]() experimentos.
experimentos.
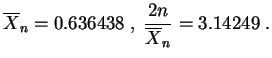
Ellos corresponden a los intervalos siguientes para ![]() :
: