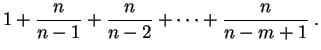Sección : modelos probabilistas
Previo : Intervalos de confianza
Siguiente : Índice
Hemos querido evitar los ejercicios clásicos de
probabilidad a base de problemas de urnas o de variables
aleatorias abstractas. El énfasis está, más bien, en la
comprensión concreta y algorítmica de las nociones del curso,
insistiendo en la verificación experimental de los cálculos de
probabilidades. Para programar los algoritmos simples que se
proponen, aconsejamos utilizar un sistema del tipo de Scilab.
Ejercicio 3
Se considera el algoritmo siguiente, donde
Int denota la
parte entera.
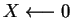
Repetir
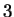
veces
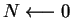
Repetir
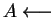
Int
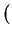
Random
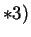
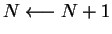
Hasta que (
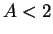
)
Si (
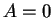
) entonces
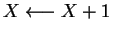
finSi
finRepetir.
- ¿Cuál es la ley de la variable aleatoria
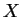 ?
?
- Calcular la probabilidad del evento
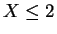 .
.
- ¿Cuál es la
ley de la variable aleatoria
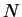 ?
?
- ¿Cuál es su esperanza?
- Calcular la probabilidad del evento
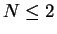 .
.
- En
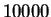 repeticiones independientes de este algoritmo, se han
observado los siguientes resultados para
repeticiones independientes de este algoritmo, se han
observado los siguientes resultados para 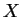 :
:
- Dar un intervalo de confianza para la probabilidad del
evento
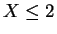 , con nivel de confianza
, con nivel de confianza 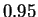 , también para
, también para
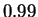 .
.
- ¿Cuantas repeticiones independientes del algoritmo
habría que realizar para que la longitud del intervalo de
confianza de nivel
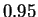 sea inferior a
sea inferior a 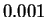 ?
?
- Dar un
intervalo de confianza para la esperanza de
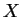 , con nivel de
confianza
, con nivel de
confianza 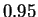 , también para
, también para 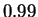 .
.
- ¿Cuantas repeticiones
independientes del algoritmo habría que realizar para que la
longitud del intervalo de confianza de nivel
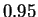 sea inferior a
sea inferior a
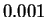 ?
?
- En
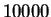 repeticiones independientes de este algoritmo, se
han observado los siguientes resultados para
repeticiones independientes de este algoritmo, se
han observado los siguientes resultados para 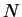 :
:
- Dar un intervalo de confianza para la probabilidad del
evento
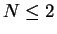 , con nivel de confianza
, con nivel de confianza 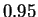 , también para
, también para
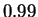 .
.
- ¿Cuantas repeticiones independientes del algoritmo
habría que realizar para que la longitud del intervalo de
confianza de nivel
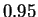 sea inferior a
sea inferior a 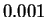 ?
?
- Dar un
intervalo de confianza para la esperanza de
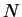 , con nivel de
confianza
, con nivel de
confianza 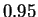 , también para
, también para 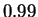 .
.
- ¿Cuantas repeticiones
independientes del algoritmo habría que realizar para que la
longitud del intervalo de confianza de nivel
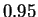 sea inferior a
sea inferior a
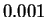 ?
?
Ejercicio 6
El objeto de estudio de este ejercicio es la paradoja de Bertrand
(sección
2.1), que como vimos es el estudio de modelos
diferentes para la selección aleatoria de una cuerda en el disco
unitario. Describimos a continuación diferentes modelos, aunque
puede haber otros modelos posibles.
- Los dos extremos de la cuerda son independientes,
de ley uniforme sobre la circunferencia.
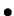
- Sea
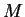 un punto de ley uniforme en el disco. La
cuerda es la intersección con el disco de la perpendicular en
un punto de ley uniforme en el disco. La
cuerda es la intersección con el disco de la perpendicular en 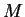 al radio
al radio 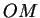 , donde
, donde 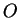 es el centro de la circunferencia.
es el centro de la circunferencia.
- Sea
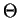 un ángulo de ley uniforme en
un ángulo de ley uniforme en
![$ [0,2\pi]$](img745.gif) y
y 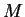 un punto de ley uniforme sobre el radio de ángulo
un punto de ley uniforme sobre el radio de ángulo
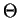 con respecto a una dirección de referencia. La cuerda es
la intersección con el disco de la perpendicular en
con respecto a una dirección de referencia. La cuerda es
la intersección con el disco de la perpendicular en 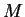 a este
radio.
a este
radio.
- Seat
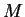 un punto de ley uniforme en el disco y
un punto de ley uniforme en el disco y
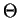 un ángulo de ley uniforme en
un ángulo de ley uniforme en ![$ [0,2\pi]$](img745.gif) (independiente de
(independiente de
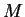 ). La cuerda es la intersección con el disco de la recta que
pasa por
). La cuerda es la intersección con el disco de la recta que
pasa por 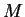 , que forma un ángulo
, que forma un ángulo 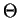 con una dirección de
referencia.
con una dirección de
referencia.
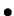
- Sea
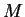 un punto de ley uniforme en la
circunferencia y
un punto de ley uniforme en la
circunferencia y 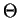 un ángulo de ley uniforme en
un ángulo de ley uniforme en ![$ [0,2\pi]$](img745.gif) ,
independiente de
,
independiente de 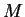 . La cuerda es la intersección con el disco de
la recta que pasa por
. La cuerda es la intersección con el disco de
la recta que pasa por 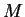 , que forma un ángulo
, que forma un ángulo 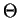 con una
dirección de referencia.
con una
dirección de referencia.
- Sean dos puntos independientes de ley uniforme en
el disco. La cuerda es la intersección con el disco de la recta
que pasa por esos dos puntos.
- Sea
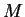 un punto de ley uniforme sobre la
circunferencia y
un punto de ley uniforme sobre la
circunferencia y 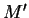 otro punto independiente del primero, con
ley uniforme en el disco. La cuerda es la intersección con el
disco de la recta que pasa por esos dos puntos.
otro punto independiente del primero, con
ley uniforme en el disco. La cuerda es la intersección con el
disco de la recta que pasa por esos dos puntos.
Para cada modelo:
- Implementar un algoritmo de simulación.
- Para una
muestra de tamaño
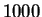 , representar un histograma de los valores
obtenidos para la longitud de la cuerda.
, representar un histograma de los valores
obtenidos para la longitud de la cuerda.
- Para la misma
muestra, dar un intervalo de confianza de nivel
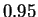 para la
esperanza de la longitud.
para la
esperanza de la longitud.
- Simular el modelo de forma tal de
obtener un intervalo de confianza para la probabilidad de que la
longitud de la cuerda sea mayor que
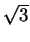 , con nivel
, con nivel 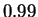 ,
cuya amplitud sea estrictamente menor que
,
cuya amplitud sea estrictamente menor que 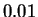 .
.
- En la
medida en que sea posible, justificar los resultados obtenidos con
un razonamiento matemático.
Ejercicio 11
Sea
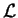
una de las leyes cuyas densidades ponemos a
continuación.
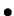
- Densidad de la ley de Weibull de parámetros
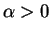 y
y 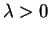 .
.
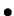
- Densidad de la ley beta
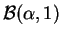 , el
parámetro
, el
parámetro 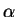 es
es 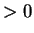 .
.
- Densidad de la ley de Pareto de parámetros
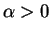 y
y 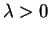 .
.
Para la ley
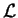
:
- Determinar la función de distribución
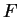 y la función
cuantil
y la función
cuantil 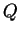 .
.
- Determinar los intervalos de dispersión de
nivel
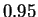 y
y 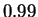 unilaterales, simétricos y optimales.
unilaterales, simétricos y optimales.
- Sea
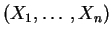 una
una 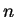 -tupla de variables aleatorias
independientes y con una misma ley continua (cualquiera). Se
denota por:
los estadígrafos de orden (valores de las
-tupla de variables aleatorias
independientes y con una misma ley continua (cualquiera). Se
denota por:
los estadígrafos de orden (valores de las 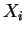 ordenados en
orden creciente). Para
ordenados en
orden creciente). Para
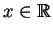 , se denota por
, se denota por 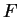 a la función
de distribución de
a la función
de distribución de 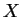 y por
y por 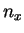 a la parte entera de
a la parte entera de 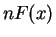 .
Emplear la Ley de los Grandes Números para demostrar que para todo
.
Emplear la Ley de los Grandes Números para demostrar que para todo
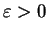 :
:
- Si
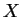 tiene por función de distribución a
tiene por función de distribución a 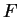 , determinar
la ley de
, determinar
la ley de 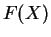 . Para
. Para
![$ u\in [0,1]$](img459.gif) , se denota por
, se denota por 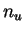 a la
parte entera de
a la
parte entera de 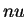 . Demostrar que para todo
. Demostrar que para todo
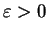 :
:
- Para la ley
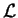 del inicio del enunciado, seleccionar
valores de los parámetros, implementar el algoritmo de simulación
por inversión, y simular variables independientes
del inicio del enunciado, seleccionar
valores de los parámetros, implementar el algoritmo de simulación
por inversión, y simular variables independientes
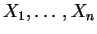 de ley
de ley 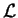 , para
, para 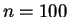 y
y 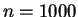 . Superponer en un mismo
gráfico una representación de la función de distribución
. Superponer en un mismo
gráfico una representación de la función de distribución 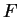 , y
los
, y
los 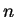 puntos de coordenadas
puntos de coordenadas
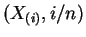 .
.
Sección : modelos probabilistas
Previo : Intervalos de confianza
Siguiente : Índice
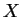 pertenece a
pertenece a
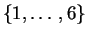 .
.
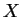 .
.
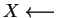 Int(Random
Int(Random 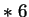 )
)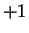
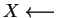 Round(Random
Round(Random 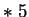 )
)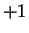
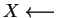 Int(Random
Int(Random 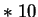 )
)
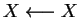 Mod
Mod 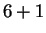
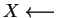 Int(Random
Int(Random 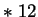 )
)
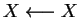 Mod
Mod 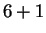
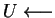 Random
Random
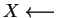 Int(
Int(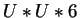 )
)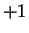
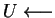 Random
Random  Random
Random
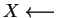 Int(
Int(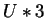 )
)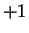
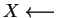 Int(Random
Int(Random 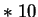 )
) 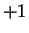
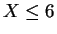 )
)
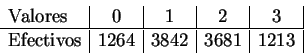
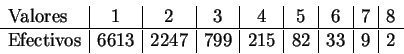
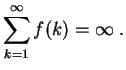
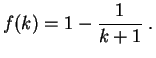
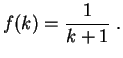
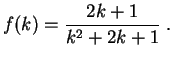
![$\displaystyle \mathbb {P}[\,A_1\bigcup\ldots\bigcup A_n\,] =
\sum_{\{i_1,\ldot...
...\dots,n\}}
(-1)^{k+1}\mathbb {P}[\,A_{i_1}\bigcap\ldots\bigcap A_{i_k}\,]\;.
$](img759.gif)