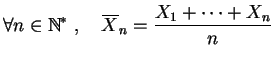 y
y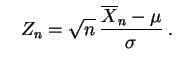
La ley de ![]() converge a la
ley normal
converge a la
ley normal
![]() , es decir para todo
, es decir para todo ![]() :
:
![$\displaystyle \lim_{n\rightarrow\infty}\,\mathbb {P}[a<Z_n<b]\;=\;
\int_a^b \frac{1}{\sqrt{2\pi}}e^{-x^2/2}\,dx
\;.
$](img631.gif)
En simulación, la situación típica es aquella en la que uno ejecuta un gran número de veces un lazo, calculando en cada pasada la realización de variables aleatorias independientes. El resultado que esperamos obtener es en general estimar una esperanza. También en simulación, como sucede en la Física o en la Biología, debemos dar un resultado indicando su exactitud. El Teorema del Límite Centrado es el que nos permite calcular esta exactitud.
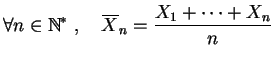 y
y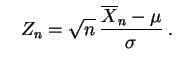
La ley de ![]() converge a la
ley normal
converge a la
ley normal
![]() , es decir para todo
, es decir para todo ![]() :
:
![$\displaystyle \lim_{n\rightarrow\infty}\,\mathbb {P}[a<Z_n<b]\;=\;
\int_a^b \frac{1}{\sqrt{2\pi}}e^{-x^2/2}\,dx
\;.
$](img631.gif)
Interpretación:
En el
Teorema
del Límite Centrado, ![]() es el valor que hay que estimar. Los
es el valor que hay que estimar. Los ![]() valores
valores
![]() constituyen una
muestra de mediciones aleatorias
independientes de
esperanza
constituyen una
muestra de mediciones aleatorias
independientes de
esperanza ![]() . La cantidad
. La cantidad
![]() es la
media empírica de la muestra, la cual
según la
Ley de los Grandes Números debe converger a la esperanza
es la
media empírica de la muestra, la cual
según la
Ley de los Grandes Números debe converger a la esperanza
![]() . El
Teorema del Límite Centrado da la exactitud de esta
aproximación. Podemos leerlo intuitivamente de la siguiente
manera. Si
. El
Teorema del Límite Centrado da la exactitud de esta
aproximación. Podemos leerlo intuitivamente de la siguiente
manera. Si ![]() es lo suficientemente grande entonces
es lo suficientemente grande entonces ![]() se
encuentra muy probablemente comprendida entre
se
encuentra muy probablemente comprendida entre ![]() y
y ![]() (la
probabilidad es
(la
probabilidad es ![]() ). Tenemos además:
). Tenemos además:
![$\displaystyle \frac{X_1+\cdots +X_n}{n} - \mu\;\in\;
\left[-\frac{3\sigma}{\sqrt n}\;;\;
+\frac{3\sigma}{\sqrt n}\right]
\;,
$](img634.gif)
El Teorema del Límite Centrado se utiliza para valores finitos de
![]() . La idea concreta es la siguiente. Si
. La idea concreta es la siguiente. Si ![]() es lo
suficientemente grande, la variable
centrada y reducida (esperanza
0 y varianza
es lo
suficientemente grande, la variable
centrada y reducida (esperanza
0 y varianza ![]() )
) ![]() asociada a la suma de
asociada a la suma de ![]() variables
independientes sigue aproximadamente la ley
variables
independientes sigue aproximadamente la ley
![]() . Si se
realiza una cantidad suficiente de simulaciones de
. Si se
realiza una cantidad suficiente de simulaciones de ![]() y si
trazamos un histograma de los valores obtenidos, este no estará
muy alejado de la curva
y si
trazamos un histograma de los valores obtenidos, este no estará
muy alejado de la curva
![]() . No más
lejos en todo caso que si hubiésemos simulado variables aleatorias
de ley
. No más
lejos en todo caso que si hubiésemos simulado variables aleatorias
de ley
![]() . Si
. Si ![]() sigue la ley
sigue la ley
![]() ,
entonces
,
entonces
![]() sigue la ley
sigue la ley
![]() .
.
También podemos decir que para ![]() lo suficientemente grande una
suma de
lo suficientemente grande una
suma de ![]() variables aleatorias independientes sigue
aproximadamente una ley normal, cuya esperanza y cuya varianza son
respectivamente la suma de las esperanzas y la suma de las
varianzas de las variables que se suman. El problema es saber a
partir de qué valor
variables aleatorias independientes sigue
aproximadamente una ley normal, cuya esperanza y cuya varianza son
respectivamente la suma de las esperanzas y la suma de las
varianzas de las variables que se suman. El problema es saber a
partir de qué valor ![]() es ``lo suficientemente grande'', para
obtener la exactitud que se desea. Esto depende mucho de la ley
de las
es ``lo suficientemente grande'', para
obtener la exactitud que se desea. Esto depende mucho de la ley
de las ![]() . La aproximación es mejor según que esta ley
sea más simétrica. En particular el buen comportamiento de
la ley uniforme, a la vista de lo que plantea el Teorema
del Límite Centrado, conduce a un algoritmo aproximado de simulación para
la ley
. La aproximación es mejor según que esta ley
sea más simétrica. En particular el buen comportamiento de
la ley uniforme, a la vista de lo que plantea el Teorema
del Límite Centrado, conduce a un algoritmo aproximado de simulación para
la ley
![]() .
.
![]()
Repetir ![]() veces
veces
![]() Random
Random
finRepetir
Justificación:
Si ![]() designa la sucesión de llamadas de
Random
(sucesión de variables independientes de
ley uniforme
en
designa la sucesión de llamadas de
Random
(sucesión de variables independientes de
ley uniforme
en ![]() , se tiene:
, se tiene:
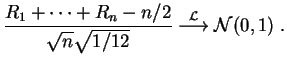
Se evita una división y se obtiene una aproximación que ya es
buena tomando ![]() . Este algoritmo no es aconsejado su empleo
con los generadores clásicos. Su inconveniente principal es que
realiza muchas llamadas a
Random, lo que plantea el problema
de la independencia de las realizaciones sucesivas. Para las leyes
más disimétricas como la
ley exponencial, la
aproximación normal no es válida para la suma de algunas decenas
de variables. Se puede considerar justificada a partir de la suma
de algunos centenares. En
simulación, son miles, si no millones,
de variables que son engendradas, y el usar la aproximación normal
es completamente legítimo.
. Este algoritmo no es aconsejado su empleo
con los generadores clásicos. Su inconveniente principal es que
realiza muchas llamadas a
Random, lo que plantea el problema
de la independencia de las realizaciones sucesivas. Para las leyes
más disimétricas como la
ley exponencial, la
aproximación normal no es válida para la suma de algunas decenas
de variables. Se puede considerar justificada a partir de la suma
de algunos centenares. En
simulación, son miles, si no millones,
de variables que son engendradas, y el usar la aproximación normal
es completamente legítimo.