La función cuantil de una variable aleatoria (o de una ley de probabilidad) es la inversa de su función de distribución. Cuando la función de distribución es estrictamente creciente, su inversa está definida sin ambigŁedad. Pero una función de distribución se mantiene constante en todo intervalo en el cual la variable aleatoria no puede tomar valores. Es por esto que se introduce la siguiente definición.
Leyes
discretas.
La función cuantil de una variable aleatoria discreta
es una función en escalera, al igual que su función de
distribución. Si ![]() toma los valores
toma los valores
![]() ,
puestos en orden creciente, la función de distribución es igual a:
,
puestos en orden creciente, la función de distribución es igual a:
![\begin{displaymath}
Q_X(u)=\left\{
\begin{array}{lcl}
x_1&&\mbox{para } u\in ...
...para } u\in ]F_k,F_{k+1}]\\
\vdots&&
\end{array}
\right.
\end{displaymath}](img435.gif)
Leyes continuas.
Vamos a situarnos en el caso
más frecuente, en el que la densidad ![]() es estrictamente
creciente en un intervalo de
es estrictamente
creciente en un intervalo de
![]() (su soporte) y nula fuera de
él. Si el intervalo es
(su soporte) y nula fuera de
él. Si el intervalo es ![]() , la función de distribución se
anula antes de
, la función de distribución se
anula antes de ![]() , si
, si ![]() es finito, crece estrictamente de 0 a
es finito, crece estrictamente de 0 a
![]() entre
entre ![]() y
y ![]() y vale
y vale ![]() después de
después de ![]() , si
, si ![]() es finito.
Todo valor
es finito.
Todo valor ![]() estrictamente comprendido entre 0 y
estrictamente comprendido entre 0 y ![]() se
alcanza una vez y una sola por
se
alcanza una vez y una sola por ![]() . El valor de
. El valor de ![]() es el
único punto
es el
único punto ![]() , comprendido entre
, comprendido entre ![]() y
y ![]() , tal que
, tal que
![]() .
.
Calculemos como ejemplo la función cuantil de la
ley exponencial
![]() , con función de distribución
, con función de distribución
![]() . Para todo
. Para todo
![]() :
:
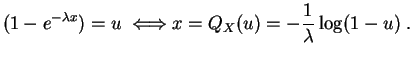
La función cuantil es un instrumento para
describir la dispersión de una ley. Si se realizan un gran número
llamadas independientes de la misma ley (obtención de una
muestra), se debe esperar que una proporción ![]() de los valores
sea inferior a
de los valores
sea inferior a ![]() . Un valor importante es la mediana,
. Un valor importante es la mediana,
![]() . Los valores de la función cuantil son empleados más
frecuentemente en estadística que los valores de la función de
distribución. Se utiliza frecuentemente en especial los
intervalos de dispersión, entendiendo esto como que deben
contener una proporción grande de los datos.
. Los valores de la función cuantil son empleados más
frecuentemente en estadística que los valores de la función de
distribución. Se utiliza frecuentemente en especial los
intervalos de dispersión, entendiendo esto como que deben
contener una proporción grande de los datos.
En estadística emplear números reales ![]() entre 0 y
entre 0 y ![]() constituye una tradición. La misma tradición hace que se les
asigne prioritariamente los valores
constituye una tradición. La misma tradición hace que se les
asigne prioritariamente los valores ![]() y
y ![]() , menos
frecuentemente
, menos
frecuentemente ![]() ,
, ![]() ó
ó ![]() . Por tanto debemos leer
. Por tanto debemos leer
![]() como ``una proporción débil'', y
como ``una proporción débil'', y
![]() como ``una
proporción fuerte''. Un
intervalo de dispersión de nivel
como ``una
proporción fuerte''. Un
intervalo de dispersión de nivel
![]() para
para ![]() es uno tal que
es uno tal que ![]() pertenece a ese
intervalo con probabilidad
pertenece a ese
intervalo con probabilidad
![]() : el contiene, por tanto,
a una fuerte proporción de la densidad, aún si el es, en general,
mucho más pequeño que el soporte de la ley. Existen, en general,
una infinidad de intervalos de dispersión de un nivel dado.
: el contiene, por tanto,
a una fuerte proporción de la densidad, aún si el es, en general,
mucho más pequeño que el soporte de la ley. Existen, en general,
una infinidad de intervalos de dispersión de un nivel dado.
Presentamos algunos de nivel ![]() para la ley normal
para la ley normal
![]() .
.

Según sean los valores de ![]() , decimos que un intervalo de
dispersión de nivel
, decimos que un intervalo de
dispersión de nivel
![]() es:
es:
Determinar un intervalo de dispersión optimal requiere, en
general, de un cálculo especial salvo en el caso en que la ley es
simétrica, como una
ley
normal o una
ley
de Student.
Decimos que
la ley de ![]() es simétrica si para todo
es simétrica si para todo
![]() ,
,
Se demuestra que si la ley de ![]() es simétrica, entonces el
intervalo de dispersión simétrico es optimal. Otra aplicación importante de la función cuantil es el método de
inversión, el cual es un método general que consiste en
simular
una variable aleatoria de cualquier ley, combinando el empleo de
la función Random con el de la función cuantil de la
variable.
es simétrica, entonces el
intervalo de dispersión simétrico es optimal. Otra aplicación importante de la función cuantil es el método de
inversión, el cual es un método general que consiste en
simular
una variable aleatoria de cualquier ley, combinando el empleo de
la función Random con el de la función cuantil de la
variable.
Demostración : Para todo
![]() , tenemos:
, tenemos:
Ejemplo :
La función cuantil de la
ley
exponencial
![]() hace corresponder a
hace corresponder a ![]() el
valor:
el
valor:
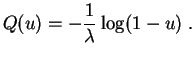
![]() Random
Random![]()
No vale la pena calcular
![]() Random
Random![]() porque Random y
porque Random y ![]() Random tienen
la misma ley.
Random tienen
la misma ley.
El método de inversión no es exacto, a menos que se conozca la
expresión explícita de ![]() , como es el caso de la ley
exponencial. Esto raramente sucede. Si queremos aplicar el método
a la ley normal, por ejemplo, será necesario utilizar un algoritmo
de aproximación. Además de la imprecisión, el método de inversión
será relativamente lento. Aún cuando se conoce explícitamente la
expresión de
, como es el caso de la ley
exponencial. Esto raramente sucede. Si queremos aplicar el método
a la ley normal, por ejemplo, será necesario utilizar un algoritmo
de aproximación. Además de la imprecisión, el método de inversión
será relativamente lento. Aún cuando se conoce explícitamente la
expresión de ![]() , el método de inversión es raramente el más
eficaz para las variables continuas. Sin embargo es
aplicable a gran cantidad de leyes discretas.
, el método de inversión es raramente el más
eficaz para las variables continuas. Sin embargo es
aplicable a gran cantidad de leyes discretas.
Supongamos que ![]() toma los valores
toma los valores
![]() , ordenados
por orden creciente. Denotemos por
, ordenados
por orden creciente. Denotemos por ![]() el valor de la función de
distribución en el intervalo
el valor de la función de
distribución en el intervalo
![]() . El algoritmo de
simulación por inversión es el siguiente.
. El algoritmo de
simulación por inversión es el siguiente.
![]()
![]() Random
Random
MientrasQue (![]() )
)
![]()
finMientrasQue
![]()
Modifiquemos ligeramente el algoritmo añadiéndole una
interpolación lineal. Cuando ![]() cae en el intervalo
cae en el intervalo
![]() , en lugar de dar
, en lugar de dar ![]() , como inicialmente, ahora
va a dar el valor:
, como inicialmente, ahora
va a dar el valor:
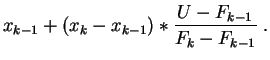
El resultado es reemplazar la función de distribución en escalera
por una función de distribución lineal a trozos que pasa por los
puntos
![]() . La distribución de probabilidad
correspondiente tiene como densidad a una función en escalera
(constante en cada intervalo
. La distribución de probabilidad
correspondiente tiene como densidad a una función en escalera
(constante en cada intervalo
![]() ). Es un
histograma.
). Es un
histograma.