![$ \displaystyle\sum\limits_{k\in K}\vert x_k\vert\mathbb {P}[X=x_k]$](img489.gif) converge,
entonces la
esperanza,
converge,
entonces la
esperanza,
A partir de la interpretación de una ley de
probabilidad como una distribución de masa, la esperanza de
una ley de probabilidad es el baricentro de esta distribución de
masa.
Leyes discretas.
Consideremos una
variable aleatoria discreta ![]() , que toma sus valores en
, que toma sus valores en
![]() . Si la serie
. Si la serie
![$ \displaystyle\sum\limits_{k\in K}\vert x_k\vert\mathbb {P}[X=x_k]$](img489.gif) converge,
entonces la
esperanza,
converge,
entonces la
esperanza,
![]() , es:
, es:
![$\displaystyle \mathbb {E}[X]
=\sum\limits_{k\in K}x_k\,\mathbb {P}[X=x_k]
\;.
$](img491.gif)
Este es el baricentro de los puntos de abscisa ![]() , cada uno con
el peso
, cada uno con
el peso
![]() .
.
Leyes continuas.
Sea ![]() una variable aleatoria continua, de
densidad
una variable aleatoria continua, de
densidad ![]() sobre
sobre
![]() . Una densidad se interpreta como una distribución de masa
continua sobre
. Una densidad se interpreta como una distribución de masa
continua sobre
![]() . Sigue siendo el baricentro lo que hay que
calcular. Si la integral
. Sigue siendo el baricentro lo que hay que
calcular. Si la integral
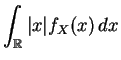 converge, entonces la
esperanza,
converge, entonces la
esperanza,
![]() , es:
, es:
![$\displaystyle \mathbb {E}[X]=\int_{\mathbb {R}}x\,f_X(x)\,dx \;.
$](img493.gif)
Demostración : La propiedad 1 es consecuencia de la linealidad de la suma
(para variables discretas) o de la integral (para variables
continuas). Demostraremos la propiedad 2 para variables
discretas.
Si, ![]() toma los valores
toma los valores
![]() ,
, ![]() toma los valores
toma los valores
![]() , como
, como ![]() e
e ![]() son independientes, el par
son independientes, el par
![]() toma los valores
toma los valores
![]() con
probabilidad
con
probabilidad
![]() . Por tanto tenemos:
. Por tanto tenemos:
![$\displaystyle \sum_{(k,h)\in K\times H}
x_k\,y_h\,\mathbb {P}[X=x_k]\,\mathbb {P}[Y=y_h]$](img502.gif) |
|||
![$\displaystyle \displaystyle\sum\limits_{k\in K}x_k\mathbb {P}[X=x_k]\,
\displaystyle\sum\limits_{h\in H}y_h\mathbb {P}[Y=y_h]$](img503.gif) |
|||
Presentamos algunos ejemplos de cálculo.
Este valor corresponde con el orden de magnitud esperado del
número de éxitos en ![]() tentativas si la probabilidad de éxito es
tentativas si la probabilidad de éxito es
![]() .
.
![$\displaystyle \mathbb {E}[X]
=\sum\limits_{k=1}^\infty k\,p\,(1-p)^{k-1}
=\frac{1}{p}
\;.
$](img508.gif)
El número de veces que se ejecuta un lazo con la salida del lazo
determinada por un test aleatorio (con probabilidad de salida
![]() ), sigue la ley
), sigue la ley
![]() . El numero medio de veces que se
ejecuta el lazo es
. El numero medio de veces que se
ejecuta el lazo es ![]() . En
. En ![]() repeticiones, el orden de
magnitud de pases será
repeticiones, el orden de
magnitud de pases será ![]() . Por ejemplo:
. Por ejemplo:
supone como promedio ![]() llamadas de la función Random.
llamadas de la función Random.
![$\displaystyle \mathbb {E}[X]
=\sum\limits_{k=0}^\infty ke^{-\lambda}\frac{\lam...
..._{k=1}^\infty\lambda
e^{-\lambda}\frac{\lambda^{k-1}}{(k-1)!}
=\lambda
\;.
$](img515.gif)
![$\displaystyle \mathbb {E}[X]=\int_a^bx\,dx=\frac{a+b}{2}$](img518.gif) (punto medio del segmento).
(punto medio del segmento).![$\displaystyle \mathbb {E}[X]=\lambda \int_{0}^{+\infty} xe^{-\lambda x}\,dx
=\frac{1}{\lambda}$](img519.gif) (integración por partes).
(integración por partes).![$\displaystyle \mathbb {E}[X]=\int_{-\infty}^{+\infty}\frac{x}{\sqrt{2\pi}}
\exp \left(-\frac{x^2}{2}\right)\,dx
=0 \,\,$](img520.gif) (función impar).
(función impar).![$ \forall k\in \mathbb {N} ^*\,\,\mathbb {P}[X=k]
=\displaystyle{\frac{ 6}{\pi^2}}
\displaystyle{\frac{ 1}{k^2}}$](img522.gif) .
.
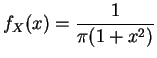 .
.
La tabla que presentamos a continuación da las esperanzas de las
leyes usuales, discretas y continuas.
Frecuentemente se encuentra el problema de calcular la esperanza
de una variable aleatoria que se expresa como función de otra
variable aleatoria, cuya ley es conocida:
![]() .
Una primera solución consiste en determinar la ley de
.
Una primera solución consiste en determinar la ley de ![]() para
después calcular su esperanza. La siguiente proposición demuestra
que esto no es necesario.
para
después calcular su esperanza. La siguiente proposición demuestra
que esto no es necesario.
![$\displaystyle \mathbb {E}[\phi(X)] = \sum_{k\in K} \phi(x_k)\mathbb {P}[X=x_k]\;.
$](img547.gif)
![$\displaystyle \mathbb {E}[\phi(X)] = \int_{\mathbb {R}} \phi(x)\,f_X(x)\,dx\;.
$](img549.gif)
Los cálculos de varianzas del próximo parrafo son una aplicación
de esta proposición.