| Home | Gallery | CV | Visit | Publications |
Branched Transport
in collaboration with F. Santambrogio
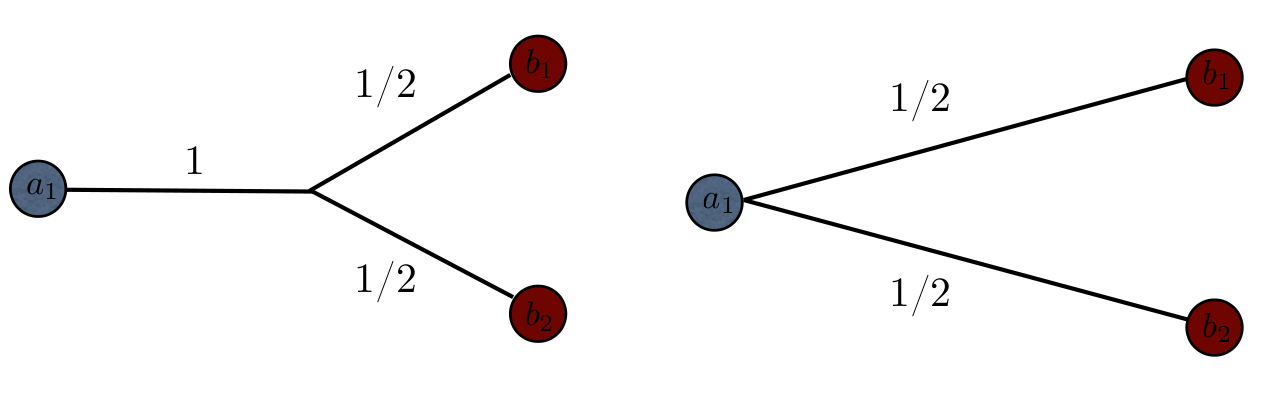
We present on this page some preliminary results on optimal irrigation problems obtained in collaboration with Filippo Santambrogio. We refer to A Modica-Mortola approximation for branched transport and applications for additional details. Such optimal irrigation networks received a large attention last years (see for instance the articles of Xia, Bernot, Maddalena, Morel, Santambrogio and Solimini). Many qualitative results and generalization of the problem have been discussed. Nevertheless, it is surprising that very few has been done on the numerical approximation of optimal networks. One explanation is given by the fact that the exact identification of global optimal networks, in the combinatorial context (see below), is known to be NP hard (with respect to the number of dirac measures).
|
In order to tackle this difficulty we introduced a new continuous framework based on a  -convergence result obtained recently by F. Santambrogio which leads to a very efficient numerical procedure. Let us introduce first this kind of problem in a discrete setting. Consider a compact convex domain
-convergence result obtained recently by F. Santambrogio which leads to a very efficient numerical procedure. Let us introduce first this kind of problem in a discrete setting. Consider a compact convex domain  and two measures which are sum of dirac masses :
and two measures which are sum of dirac masses :
![\[ s = \sum_{i=1}^m a_i \,\delta_{x_i} \,\, \text{and} \,\, g = \sum_{j=1}^n b_j \, \delta_{y_j} \]](form_2.png)
where  and
and 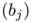 are positive numbers. We ask to
are positive numbers. We ask to 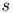 and
and 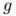 to have the same total mass, that is
to have the same total mass, that is 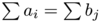 . Following Xia, we define a transport path
. Following Xia, we define a transport path 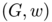 from
from 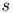 to
to 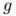 as both a weighted directed graph $G$ which vertices contains the points
as both a weighted directed graph $G$ which vertices contains the points 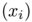 and
and 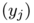 and a weight function
and a weight function 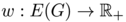 where
where 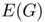 is the set of directed edges of
is the set of directed edges of 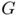 . Moreover we ask
. Moreover we ask 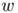 to satisfy Kirchhoff's law that is for all vertex
to satisfy Kirchhoff's law that is for all vertex 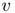 of
of 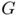 we have:
we have:
![\[ \sum_{e\in E(G),\, e^- = v} w(e)= \sum_{e\in E(G),\, e^+ = v} w(e) + \left\{ \begin{array}{rl} \displaystyle a_i & \text{if $v = x_i$ for some} \; i\\ -b_j & \text{if $v = y_j$ for some} \; j \\ 0 & \text{otherwise} \end{array} \right . \]](form_16.png)
where 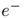 and
and 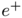 denote the starting and ending points of each directed edge
denote the starting and ending points of each directed edge 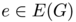 . To every transport path
. To every transport path 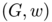 we associate a cost of transportation defined by
we associate a cost of transportation defined by
![\[ M_{\alpha}(G) = \sum_{e\in E(G)} w(e)^\alpha \;\text{length}(e) \]](form_20.png)
for some fixed parameter ![$\alpha \in [0,1] $](form_21.png) .
.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
We recall below how this discrete problem can be translated in a continuous context and the main 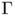 -convergence obtained by F. Santambrogio. Let
-convergence obtained by F. Santambrogio. Let 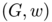 be a transport path associated to the two measures
be a transport path associated to the two measures 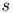 and
and 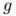 . In order to introduce a relaxed formulation to the previous problem we associate to every
. In order to introduce a relaxed formulation to the previous problem we associate to every 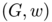 the vectorial measure
the vectorial measure
![\[\displaystyle u_G = \sum_{e \in E(G)} w(e) \, \frac{e^+ - e^-}{||e^+ - e^-||} \mathcal{H}^1_{\vert e}.\]](form_22.png)
By definition, the measure 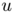 is in the class of vectorial measures of the type
is in the class of vectorial measures of the type 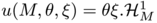 , where
, where 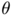 and
and 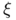 are respectively a positive function and a unit vector field defined on
are respectively a positive function and a unit vector field defined on 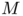 a set of finite
a set of finite 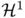 -Hausdorff measure. Moreover Kirchhoff's law in this continuous setting is equivalent to the divergence constraint
-Hausdorff measure. Moreover Kirchhoff's law in this continuous setting is equivalent to the divergence constraint
![\[\nabla . u = g - s.\]](form_29.png)
In a analogous way to (costalpha}) we define for every vectorial measure 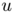 the cost functional:
the cost functional:
![\[ M^\alpha (u) = \left\{ \begin{array}{l} \int_M \theta ^\alpha \, d \mathcal{H}^1 \; \text{if $u$ is of the type $u(M,\theta,\xi)$ } \\ + \infty \;\;\text{otherwise} \end{array} \right . \]](form_30.png)
Thus, our relaxed optimisation problem is to minimise 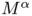 under the previous (weak) divergence constraint. The
under the previous (weak) divergence constraint. The 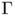 -convergence result we are going to present is based on functionals very similar to the ones of Modica and Mortola but of the form
-convergence result we are going to present is based on functionals very similar to the ones of Modica and Mortola but of the form
![\[ \displaystyle E_\varepsilon(u) = \varepsilon^{\gamma_1} \int _\Omega | u|^\beta + \varepsilon^{\gamma_2} \int _\Omega |\nabla u|^2\]](form_32.png)
defined on 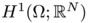 with
with 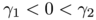 . The main difference with Modica and Mortola's functionnal is the fact that the double-well potential has been replaced by a concave power
. The main difference with Modica and Mortola's functionnal is the fact that the double-well potential has been replaced by a concave power 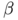 which forces the modulus of the vector field
which forces the modulus of the vector field 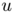 to tends to
to tends to 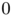 or
or 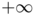 . The idea is now to choose the parameters
. The idea is now to choose the parameters 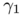 ,
, 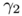 and
and 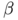 to obtain a functional equivalent (asymptotically when
to obtain a functional equivalent (asymptotically when 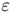 tends to
tends to 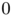 ) to the cost (costcont}). Considering that the support of
) to the cost (costcont}). Considering that the support of 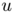 is concentrated on a segment, an heuristic argument leads to the following choice of the parameters :
is concentrated on a segment, an heuristic argument leads to the following choice of the parameters :
![\[ \beta = \frac{2-2N + 2 \alpha N}{3-N + \alpha(N-1)},\;\;\frac{\gamma_1}{\gamma_2}=\frac{(N-1)(\alpha-1)}{3-N + \alpha(N-1)} \]](form_41.png)
Let us call 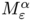 the functional associated to a set of parameters satisfying conditions (paramirrig}). F.
the functional associated to a set of parameters satisfying conditions (paramirrig}). F.
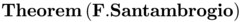 : Suppose
: Suppose 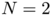 and
and ![$\alpha \in ]1/2,1[$](form_45.png) . Then
. Then 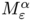
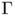 -converges to
-converges to 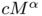 with respect to the convergence of measures for some suitable constant
with respect to the convergence of measures for some suitable constant 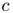 when
when 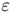 tends to
tends to 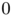 .
.
The previous 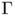 -convergence result makes it possible to replace an hard discrete problem by a sequence of optimisation problems under linear constraints. In addition, we observed that for
-convergence result makes it possible to replace an hard discrete problem by a sequence of optimisation problems under linear constraints. In addition, we observed that for 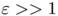 the functional
the functional 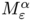 is close from being convex. This observation was the starting point of our optimisation strategy. The main difference between this situation and the previous one is related to the divergence constraint. Due to the very simple structure of the constraints we had to deal with, it was straightforward to compute a projection on the linear constraints in the context.
is close from being convex. This observation was the starting point of our optimisation strategy. The main difference between this situation and the previous one is related to the divergence constraint. Due to the very simple structure of the constraints we had to deal with, it was straightforward to compute a projection on the linear constraints in the context.
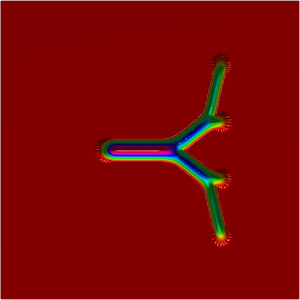
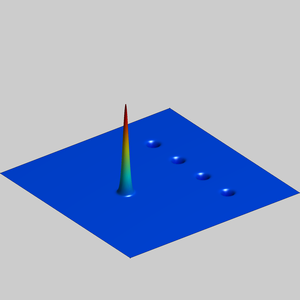
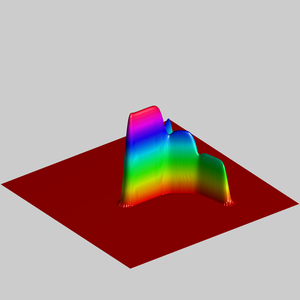
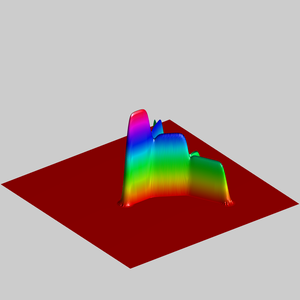
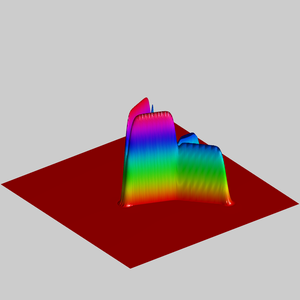
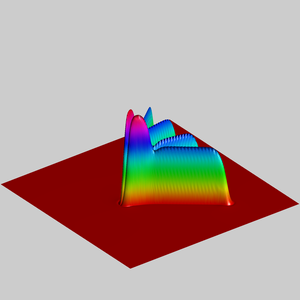
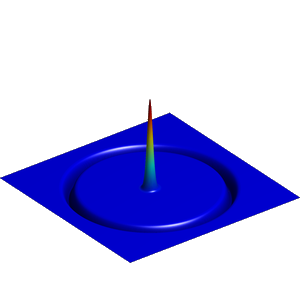
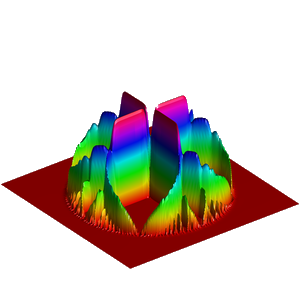
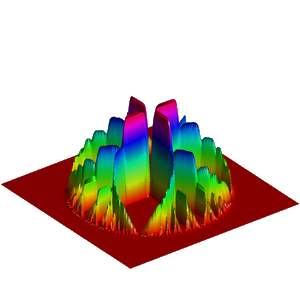
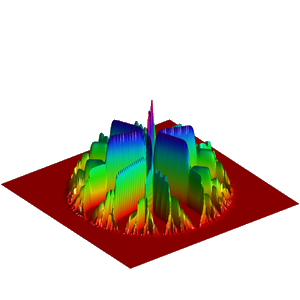
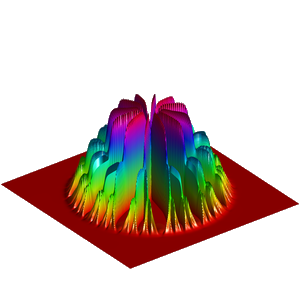
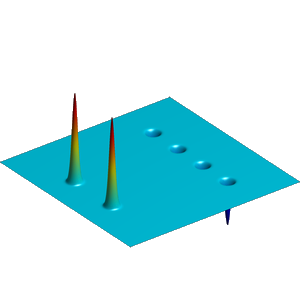
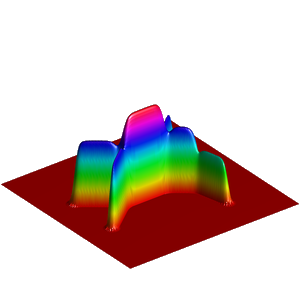
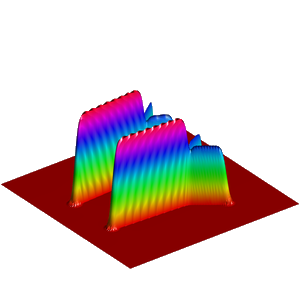
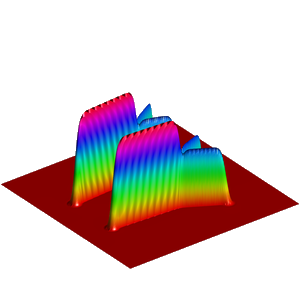
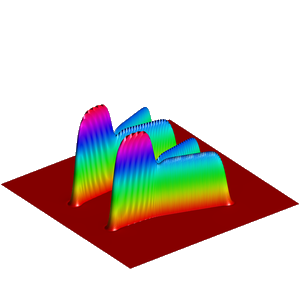
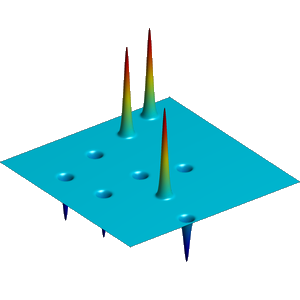
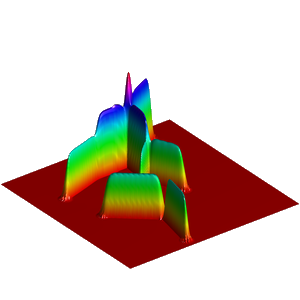
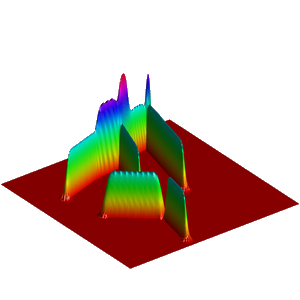
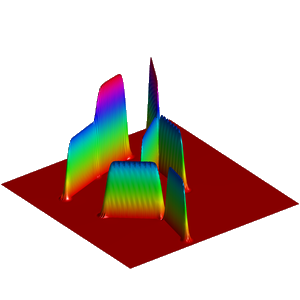
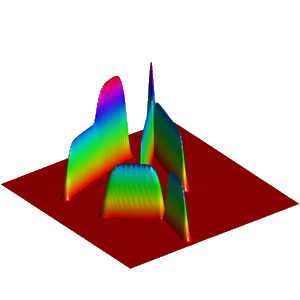
We present below the first results obtained with our simple approach. The following figures are the results of four different experiments with two different values of the parameter 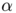 . On the first rows of the figures, we represent two views of the graph of the given density
. On the first rows of the figures, we represent two views of the graph of the given density 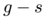 . The second rows represent two views of the graph of the norm of the optimal vector field for each value of
. The second rows represent two views of the graph of the norm of the optimal vector field for each value of 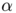 . As expected, ``Kirchhoff's law is approximatively satisfied'' by the support of the vector field which converges to a one dimensional set. Moreover we observe that two different values of
. As expected, ``Kirchhoff's law is approximatively satisfied'' by the support of the vector field which converges to a one dimensional set. Moreover we observe that two different values of 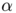 may lead to very different optimal structures.
may lead to very different optimal structures.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |