Home

Gallery

Teaching

Visit

Publications

	A calibration is a functional analytic tool developed in Calculus of Variations to prove the global optimality of a given explicitly known structure. This notion was initially introduced in the context of minimal surfaces and area minimizing and has been extended very recently by Marchese and Massaccesi to the cases of the Steiner tree and the irrigation network problems.
	Jordan, Kinderlehrer and Otto showed in 1999 how to interpret Fokker-Planck's equation as a gradient flow in the space of probability measures endowed with the Wasserstein distance. This type of formulation has proved to be a powerful tool for studying partial differential equations involving generalized diffusion terms and non-local interaction terms.
	Equilibrium multi-population matching (matching for teams) is a problem from mathematical economics which is related to multi-marginal optimal transport. A special but important case is the Wasserstein barycenter problem, which has applications in image processing and statistics.
	Optimal transport with proximal splitting (in collaboration with N. Papadakis and G. Peyré). We provide a unified non smooth convex formulation of famous Benamou and Brenier approach. Multi-dimensional Matlab code for computing continuous optimal trnasport, including fast divergence projection operator by FFT, is available.
	Handling convexity-like constraints in variational problems (in collaboration with Q. Mérigot).
	We study a free boundary problem associated to a global non-smooth convex energy. We prove qualitative results and introduce an efficient large scale optimization approach. We recover, as an asymptotic limit, the singular set of the distance function to the boundary of the domain.
	Reconstruction of a convex body from its Gaussian curvature measure. This work is based on the equivalence between this geometrical problem and an optimal transport formulation on the sphere for a specific cost of transportation (in collaboration with Q. Mérigot).
	ShapeBox is a new web interface which allows you to investigate 2D optimization problems related to shape functionals (3D will be available in the next release). Your query is submitted online, launching the computation dynamically on our server. Once the job is done, you receive an email with a link to the result webpage. Try it !
	Examples of discontinuous transport plans have been found by Luis Caffarelli between probability densities on the plane with non-convex support. Several authors studied this phenomena on convex surfaces. We investigate numerically this question and provide an explicit configuration where discontinuity happens (in collaboration with Q. Mérigot).
	Numerical study of Branched Transport Networks. Based on a functional framework introduced by Xia, we introduce a relevant relaxation and illustrate its numerical efficiency (in collaboration with F. Santambrogio).
	In this work we simply consider the Benamou-Brenier formulation assuming that the functional has a term which has a superlinear growth with respect to the density (in collaboration with G. Buttazzo and C. Jimenez).
	How to recover the boundary of a smooth object based on its digital projection ? We discuss several optimization procedure based on curvature estimates, convex analysis and phase field methods (in collaboration with E. Bretin and J-O. Lachaud).
	We discuss the optimization of eigenmodes of Dirichlet Laplacian with respect to the domain in 2D. We present the first examples of optimal profiles which are not balls or union of balls. This fact contradicts an old conjecture formulated by Polya and Szego.
	Regular hexagons have been proved by Hales to be optimal with respect to the boundary measure among unite 2D tilings. This problem is not solved in three dimension whereas Kelvin conjecture has recently been contradicted by a surprising tiling made of two kinds of irregular polytops...
	How to cut a pie of strange shape in equal pieces ?
	Many properties of constant width sets of the plane have been derived last century by different authors like Lebesgue and Blaschke. Most of these results are very difficult to extend in three dimension. Among these questions, a famous conjecture due to Meissner is still unsolved. We describe in a list of three articles several new results on constant width bodies (in collaboration with T. Lachand Robert): raising dimension, parametrization, optimality conditions, approximations, etc. (see also the page of my publications).
	Honeycomb tiling has been conjectured by Caffarelly and Lin to be asymptotically optimal (with respect to the number of cells) for the sum of first Dirichlet modes. We describe here an algorithm which is relevant in this context to avoid most of local minima to obtain a satisfactory description of optimal configurations. Implementation difficulties and parallelization are also discussed (in collaboration with B. Bourdin and D. Bucur).
	Newton's problem is famous in the field of calculus of variations for its simplicity and its difficulty ! A lot of work has been addressed to the unusual constraint of convex profile. We describe in this work a new discrete/continuous algorithm which do not assume any regularity hypothesis. A numerical approach to evaluate the Cheeger constant of a convex body is also provided (in collaboration with T. Lachand Robert).
	One strange (not always well posed...) shape optimization problem: minimization of the Dirichlet energy under volume constraints of the level sets (in collaboration with O. Rieger).
	The problem introduced in this work is now known as the "mean distance problem". It addresses the minimization of the irrigation cost of a one dimensional connected set of prescribed length. We derived qualitative properties of optimal configurations and develop a new algorithm which outputs satisfy these necessary conditions of optimality (in collaboration with G. Buttazzo and E. Stepanov).
	A convex geometry toolbox in matlab (Steiner symetrization, convex hull, etc.). This toolbox is an interface for some functions of the "qhull" library.
	Vlasov simulations can for some situations be a valuable alternative to PIC sim- ulations for the study of intense beam propagation. However, as they rely on a phase-space grid which is fixed for the whole simulation, important computing ef- fort can be wasted in zones where no particles are present at some given time. In order to overcome this drawback, we introduce here a new method which makes use of a phase-space grid which is uniform at any given time, but moves in time according to the evolution of the envelope of the beam.
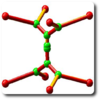	Steiner trees are fundamental objects in computational geometry. We provide a stochastic algorithm based on fast spanning tree computation which is efficient for a small number of sites (old work, be indulgent).