| Home | Gallery | CV | Visit | Publications |
Spheroforms
in collaboration with T. Lachand-Robert
A
body (that is, a compact connected subset the euclidian space) is said
to be of constant width if its projection on any straight line is a
segment of the same value for all lines.
Obvious bodies of constant width are the balls; but they are many others. These bodies, also called orbiforms in dimension two, or spheroforms in dimension three, have many interesting properties and applications. Orbiforms in particular have been studied a lot during the nineteenth century and later, particularly by Frank Reuleaux, whose name is now attached to those orbiforms you get by intersecting a finite number of disks of equal radii a, whose center are vertices of a regular polygon of diameter a. In particular the Reuleaux triangle is the intersection of three discs of radius a, centered on vertices of an equilateral triangle with side length a.
The mere existence of non trivial three-dimensional bodies of constant width is not so easy to establish. In particular, no finite intersection of balls has constant width, a striking difference with the two-dimensional case.
Meissner's tetrahedron
To obtain spheroforms, a simple construction is to consider a two dimensional body of constant width having an axis of symmetry (like the Reuleaux triangle for instance): the corresponding body of revolution obtained by rotation around this axis is a spheroform. F. Meissner was able to construct another spheroform (usually called "Meissner's tetrahedron'') which does not have the symmetry of revolution. We give in our paper cited below an alternate construction of this body.
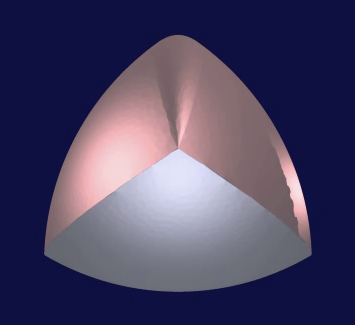 (click to get a Quicktime animated view) |
 |
| Meissner's body | |
Raising dimension
Although many properties of bodies of constant width are known, very few characterizations exist in the literature, except basic ones. The aim of our paper is to provide a number of them, that is, properties of bodies (in arbitrary dimension) that ensure they have constant width. This is important in particular for variational studies, like the still open problem of finding the orbiform of minimal volume.
As a side effect, we give in our paper a different application of these characterizations: namely we give a way to construct a body of constant width in dimension n, starting from a given projection in dimension n-1. Starting from a one-dimensional convex body (a segment), we get a two-dimensional Reuleaux triangle. Starting from a two-dimensional Reuleaux triangle, we get Meissner's body. This yields some sort of canonical construction of this body. This process can be continued to any dimension. For instance here is a four-dimensional body of constant width whose projection is Meissner's body.
 |
 |
| A four-dimensional constant width body (time shows 3d-sections) | |
All details can be found in our paper "Bodies of constant width in arbitrary dimension", by T. Lachand-Robert & É. Oudet.