Etant donné un
échantillon
observé
![]() et
une
loi de probabilité
et
une
loi de probabilité
![]() , la
vraisemblance
quantifie la
probabilité
que les observations proviennent effectivement
d'un
échantillon
(théorique) de la loi
, la
vraisemblance
quantifie la
probabilité
que les observations proviennent effectivement
d'un
échantillon
(théorique) de la loi ![]() .
.
Prenons l'exemple de 10 lancers de pièce. L'échantillon binaire observé est par exemple :
Il est naturel de choisir comme
estimation
de ![]() , celle
pour laquelle la
probabilité
de l'
échantillon
observé est la plus
forte, à savoir ici
, celle
pour laquelle la
probabilité
de l'
échantillon
observé est la plus
forte, à savoir ici ![]() 0.6.
0.6.
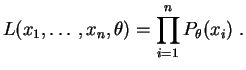
L'interprétation est la suivante. Considérons
un
échantillon
théorique
![]() de la loi
de la loi ![]() .
Par définition, les
variables aléatoires
.
Par définition, les
variables aléatoires
![]() sont
indépendantes
et de même loi
sont
indépendantes
et de même loi ![]() . Donc la probabilité
que
l'échantillon
théorique
. Donc la probabilité
que
l'échantillon
théorique
![]() ait pour réalisation
l'échantillon
observé
ait pour réalisation
l'échantillon
observé
![]() est le produit des probabilités
pour que
est le produit des probabilités
pour que ![]() prenne la valeur
prenne la valeur ![]() , à savoir :
, à savoir :
Dans le cas d'un
modèle
continu, la loi ![]() a une
densité
sur
a une
densité
sur
![]() , et la
probabilité
pour que
l'échantillon
prenne une
valeur particulière est toujours nulle. Il faut alors remplacer la
probabilité
, et la
probabilité
pour que
l'échantillon
prenne une
valeur particulière est toujours nulle. Il faut alors remplacer la
probabilité
![]() par sa
densité
dans la définition de
la
vraisemblance.
par sa
densité
dans la définition de
la
vraisemblance.
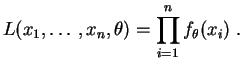
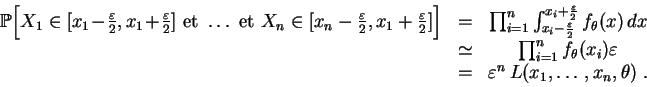
Estimer un paramètre par la méthode du
maximum de vraisemblance,
c'est proposer comme valeur de ce paramètre celle qui rend maximale
la
vraisemblance,
à savoir la
probabilité
d'observer les données
comme réalisation d'un
échantillon
de la loi ![]() .
.
On l'appelle estimation par maximum de vraisemblance.
Si
![]() est un
échantillon
(théorique) de la loi
est un
échantillon
(théorique) de la loi
![]() , la
variable aléatoire
:
, la
variable aléatoire
:
Reprenons l'exemple de la
loi uniforme
sur l'intervalle
![]() .
Sa
densité
est :
.
Sa
densité
est :
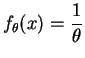 1
1
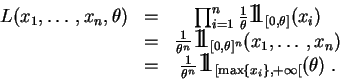
Vue comme fonction de ![]() , la
vraisemblance
est nulle si
, la
vraisemblance
est nulle si ![]() est inférieur à la plus grande des valeurs observées, elle vaut
est inférieur à la plus grande des valeurs observées, elle vaut
![]() sinon. Elle est donc maximale pour :
sinon. Elle est donc maximale pour :
Pour la plupart des lois de probabilité usuelles, l'estimateur du maximum de vraisemblance est défini de façon unique, et se calcule explicitement. Sur le plan théorique, il présente de nombreux avantages. Sous des hypothèses vérifiées par de nombreux modèles courants, on démontre qu'il est asymptotiquement sans biais et convergent. On démontre de plus que sa variance est minimale. La méthode du maximum de vraisemblance est donc théoriquement la meilleure des méthodes d'estimation. Nous verrons au paragraphe suivant des exemples de calculs explicites. Quand une détermination explicite est impossible, il faut avoir recours à une détermination numérique, par un algorithme d'optimisation.