Jusqu'ici le seul
modèle probabiliste
que nous ayons envisagé pour
des
données
observées considérait qu'elles étaient
des réalisations de
variables indépendantes
et de même loi.
Cela revient à supposer
que les individus sur lesquels les
données
ont été recueillies sont
interchangeables, et que les différences observées entre eux sont
seulement imputables
au hasard.
Dans de nombreuses situations,
on cherche à expliquer ces différences, c'est-à-dire à les
attribuer à l'effet d'autres
caractères
mesurés sur les mêmes
individus. La
modélisation
probabiliste considèrera
que la mesure (à expliquer) effectuée sur un
individu
donné
est une
variable aléatoire,
dont la loi dépend des valeurs prises
sur cet
individu
par les
caractères
explicatifs, considérés comme
déterministes. Si ![]() désigne la
variable aléatoire
associée
à
l'individu
désigne la
variable aléatoire
associée
à
l'individu
![]() , et
, et
![]() les valeurs
prises pour cet
individu
par les
caractères
explicatifs
les valeurs
prises pour cet
individu
par les
caractères
explicatifs
![]() , on séparera l'effet déterministe et l'effet
aléatoire
par un
modèle
du type :
, on séparera l'effet déterministe et l'effet
aléatoire
par un
modèle
du type :
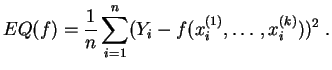
Dans certains cas classiques, on sait résoudre explicitement ce problème de minimisation, et la solution est implémentée dans les environnements de calculs statistiques. Quand une résolution explicite est impossible, on a recours à des algorithmes de minimisation, comme l'algorithme du gradient.
Le cas le plus fréquent est celui de la
régression linéaire simple,
où un seul
caractère
est explicatif, et la fonction ![]() est
affine :
est
affine :
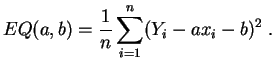
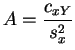 et
etLa valeur de ce minimum est :
Les
variables aléatoires
![]() et
et ![]() sont les
estimateurs
des
moindres carrés
des paramètres
sont les
estimateurs
des
moindres carrés
des paramètres ![]() et
et ![]() .
.
On peut utiliser les estimateurs des moindres carrés pour estimer les paramètres de certaines lois, dans un problème d'ajustement. Nous traitons à titre d'exemple les lois normales et les lois de Weibull.
Soit
![]() un
échantillon
de taille
un
échantillon
de taille ![]() de la
loi normale
de la
loi normale
![]() , les paramètres
, les paramètres ![]() et
et ![]() étant inconnus. Pour
étant inconnus. Pour
![]() , notons
, notons ![]() les
statistiques d'ordre
(valeurs
les
statistiques d'ordre
(valeurs ![]() ordonnées de la plus grande à la
plus petite). Si l'hypothèse
de normalité est pertinente,
alors
ordonnées de la plus grande à la
plus petite). Si l'hypothèse
de normalité est pertinente,
alors ![]() doit être proche du quantile
doit être proche du quantile
![]() de la loi
de la loi
![]() .
Rappelons que si une
variable aléatoire
.
Rappelons que si une
variable aléatoire
![]() suit la loi
suit la loi
![]() ,
alors
,
alors
![]() suit la loi
suit la loi
![]() . Ceci revient
à dire que pour tout
. Ceci revient
à dire que pour tout ![]() [0,1] :
[0,1] :
La
fonction quantile
de la
loi de Weibull
![]() est :
est :
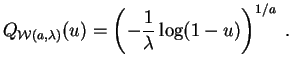
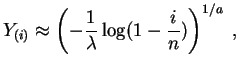
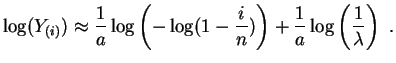
Posons
![]() et
et
![]() . Les points
. Les points
![]() devraient être proches de la droite d'équation
devraient être proches de la droite d'équation
![]() . Les
estimateurs
des
moindres carrés
. Les
estimateurs
des
moindres carrés
![]() et
et
![]() pour la
régression linéaire simple
des
pour la
régression linéaire simple
des ![]() sur les
sur les ![]() sont des
estimateurs
de
sont des
estimateurs
de ![]() et
et
![]() respectivement.
Donc
respectivement.
Donc ![]() et
et ![]() sont des
estimateurs
de
sont des
estimateurs
de ![]() et
et ![]() respectivement.
respectivement.