| Home | Gallery | CV | Visit | Publications |
Regularization of discrete contour by Willmore energy
in collaboration with E. Bretin and J-0. Lachaud
We present on this page some preliminary results on the regularization of digital contours obtained in collaboration with Elie Bretin and Jacques-Olivier Lachaud. All details can be found in our paper Regularization of discrete contour by Willmore energy.
 |
 |
 |
 |
Shapes which minimize their total squared curvature have risen a lot of interest in the mathematics community. In the 2D plane, they are known as Euler elastica, while its 3D variant is the minimization of the Willmore energy
![\[ F(\Omega) = \int_{\partial \Omega} \kappa^2 \, d\sigma. \]](form_0.png)
Recently, Kerautret and Lachaud proposed to use these shapes for reconstructing a continuous analog to digital shapes. The idea is to find among all possible euclidean shapes that have the same digitization as the digital shape of interest, the one with smallest total squared curvature. In a sense, due to its smoothness and invariance properties, this euclidean shape is a very natural one with the desired digitization. By this way, they obtain a curvature estimator with many desirable properties (accuracy, stability, robustness to noise). In this context, from two given digital constraints, the problem is to identify the optimal shape solution of
![\[ \inf_{\Omega_{int}\subset\Omega\subset \Omega_{ext}} F(\Omega). \]](form_1.png)
We begin our paper in recalling the optimization method GMC which extracts an approximated solution based on discrete geometry tools and is valid for arbitrary digital object. Then, we describe a first new method for solving previous problem which is limited to convex shapes. In this context, the problem can be reformulated into a convex programming problem with respect to the radius of curvature through the use of the support functions :
![\[ F(\Omega) = \int_{0}^{2\pi} \frac{1}{R} \, d\theta = \int_{0}^{2\pi} \left(\frac{d^2h_\Omega}{d\theta^2} + h_\Omega \right)^{-1} \, d\theta, \]](form_2.png)
under the additional constraints
![\[ \frac{d^2h_\Omega}{d\theta^2} + h_\Omega \geq 0 \,\, \text{and}\,\, h_{\Omega_{int}} \leq h_{\Omega} \leq h_{\Omega_{ext}}. \]](form_3.png)
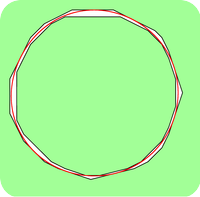 |
 |
 |
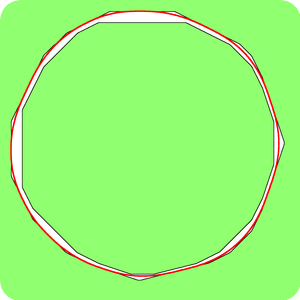 |
 |
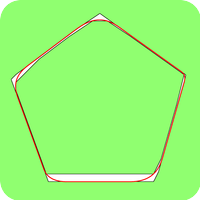 |
similar results while the second illustrates the existence of critical curves obtained by the phase field method which are not global minimizer
Our second new method, the more flexible one, is based on relaxation methods obtain by  -convergence results. More precisely, we look for an optimal density function
-convergence results. More precisely, we look for an optimal density function 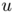 which minimizes the energy
which minimizes the energy
![\[ F_{\Omega_{int},\Omega_{ext}}(u) = \int_{R^d} \frac{1}{\varepsilon} \left( -\varepsilon \triangle u + \frac{1}{\varepsilon} \partial_u W_{\Omega_{int},\Omega_{ext}}(u,x) \right)^2 dx. \]](form_6.png)
for some potential 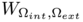 associated to the domains
associated to the domains 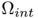 and
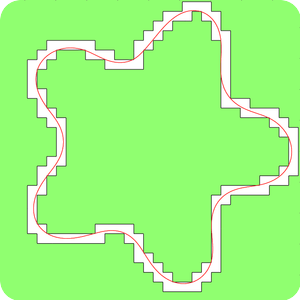
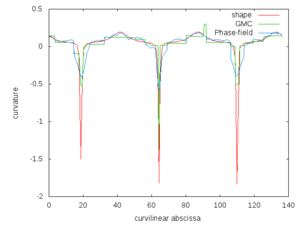
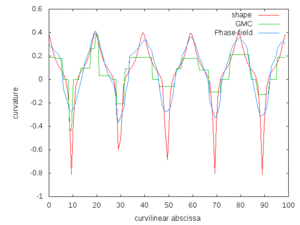
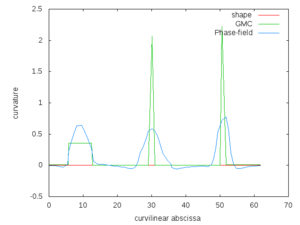
and 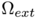 . We compared numerically the closeness of the curvature fields extracted by the GMC method and the phase field method on various shapes at two different resolutions. See our page of experiments for a complete list of our tests. The error measures are summed up on graphs below. Plots of curvature fields as well as the phase field reconstruction are given. We also included the curvature field of the euclidean shape before digitization. Notice that the euclidean shape is generally not the optimal shape for minimizing Willmore energy. Nevertheless they share many features such as smoothness and number of position of extremal points. Moreover, by definition of the digital constraints those shapes are geometrically close.
. We compared numerically the closeness of the curvature fields extracted by the GMC method and the phase field method on various shapes at two different resolutions. See our page of experiments for a complete list of our tests. The error measures are summed up on graphs below. Plots of curvature fields as well as the phase field reconstruction are given. We also included the curvature field of the euclidean shape before digitization. Notice that the euclidean shape is generally not the optimal shape for minimizing Willmore energy. Nevertheless they share many features such as smoothness and number of position of extremal points. Moreover, by definition of the digital constraints those shapes are geometrically close.
Regarding the evaluation of curvature fields obtained from GMC method and the phase field method we first notice that extremal points are consistently localized with respect to the original shape. Curvature fields of both methods are numerically close for disks and ellipses and get closer as the resolution gets finer. On the other hand the curvature field obtained by the phase field approach is far away from the original shape when considering polygons. This bad behavior is related to the fact that the Willmore energy is not relevant for extracting shapes with non smooth curvature field. In this context the GMC algorithm has a more natural output because it has a pre-processing which locates linear parts of the boundary. This avoids spurious inflexion points which have been observed in phase field reconstruction.
 |
 |
 |
 |
 |
 |