Optimal convex bodies

in collaboration with T. Lachand-Robert


Here are some of the results we got from our algorithm solving minimization problems under convexity constraints. All details can be found in our paper "Minimizing within convex bodies using a convex hull method", by T. Lachand-Robert & É. Oudet.

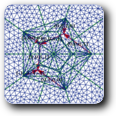
Alexandrov's problem

Given its normal vectors and the areas of its faces, we reconstruct a convex polytope. (See section 2.3 of the paper.)


An example with 1000 faces
(click to get the animated view)

Cheeger's problem

Given an enclosing convex box Q, what is the convex subset of Q which maximize the ratio volume over surface area? Except for the ball, the general answer is unknown. Here are the results we get for the cube, the tetrahedron, and the dodecahedron.


Solution for the cube
(click to get the animated view)

Solution for the tetrahedron
(click to get the animated view)
Solution for the dodecahedron
(click to get the animated view)

Newton's problem of the body of minimal resistance

The problem of the body of minimal resistance has been settled by I. Newton in its Principia: given a body progressing at constant speed in a fluid, what shape should it be given in order to minimize its resistance? This problem is described in more details in section 3 of the paper.

Our numerical profiles shown below are better than any previously conjectured optimal shapes:

M Newton's radial value best theoretical values numerical values
3/2 0.7526 0.7019 0.7012
1 1.1775 1.1561 1.1379
7/10 1.5685 1.5566 1.5457
4/10 2.1074 2.1034 2.1006

Solution for M = 0.4
(click to get the animated view)
Solution for M = 0.7
(click to get the animated view)

Solution for M = 1.0
(click to get the animated view)
Solution for M = 1.5
(click to get the animated view)