| Home | Gallery | CV | Visit | Publications |
JKO scheme and gradient flows
in collaboration with J.-D. Benamou, G. Carlier and Q. Merigot
Here are some results obtained in collaboration with J.-D. Benamou, G. Carlier and Q. Merigot. All details can be found in our paper Discretization of functionals involving the Monge-Ampère operator.
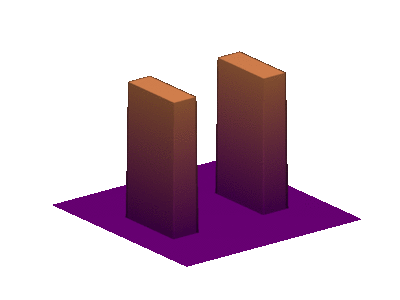
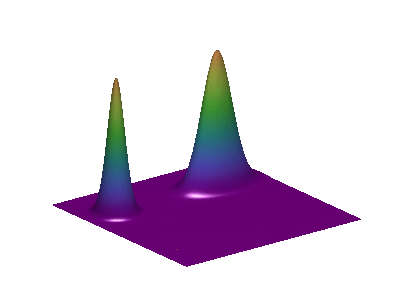
Move your mouse on the pictures to animate (slow connection be patient)
 |
 |
Jordan, Kinderlehrer and Otto showed in 1999 how to interpret Fokker-Planck's equation as a gradient flow in the space of probability measures endowed with the Wasserstein distance. This type of formulation has proved to be a powerful tool for studying partial differential equationsinvolving generalized diffusion terms and non-local interaction terms. The construction of Jordan, Kinderlehrer and Otto of the gradient flow of an energy E on the space of probability measures relies on a time-discretization through an implicit Euler scheme. A time step can be written as
![\[ \rho_1 := \text{argmin} W_2^2(\rho_0,\rho) + E(\rho), \]](form_0.png)
where 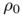 and
and 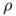 are probability measures, and
are probability measures, and 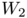 is the quadratic Wasserstein distance. Despite the potential applications, there does not exist many numerical methods for this type of scheme, and most of them are restricted to the 1D case. Letting
is the quadratic Wasserstein distance. Despite the potential applications, there does not exist many numerical methods for this type of scheme, and most of them are restricted to the 1D case. Letting 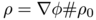 , where
, where 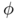 is a convex function, a timestep in the JKO scheme can be reformulated as an optimization problem over the space of convex functions. When the energy
is a convex function, a timestep in the JKO scheme can be reformulated as an optimization problem over the space of convex functions. When the energy 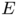 contains an entropy term, which corresponds to a diffusion term in the underlying PDE, the formulation using
contains an entropy term, which corresponds to a diffusion term in the underlying PDE, the formulation using 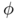 involves the Monge-Operator of
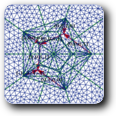
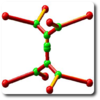
involves the Monge-Operator of 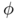 and is therefore not of the previous form. With G. Carlier, JD Benamou we introduced a space discretization of optimization problems over the space of convex functions and involving the Monge-Ampère operator. In our formulation, an entropy term is transformed into a barrier for the convexity of the discrete functions. This allows us to use Newton's method for the resolution of the discrete problem, which converges in a few iterations. We present numerical applications to the fast diffusion equation, the porous medium equation and to the simulation of crowd motion (see below).
and is therefore not of the previous form. With G. Carlier, JD Benamou we introduced a space discretization of optimization problems over the space of convex functions and involving the Monge-Ampère operator. In our formulation, an entropy term is transformed into a barrier for the convexity of the discrete functions. This allows us to use Newton's method for the resolution of the discrete problem, which converges in a few iterations. We present numerical applications to the fast diffusion equation, the porous medium equation and to the simulation of crowd motion (see below).
 |
 |
 |
 |
 |
 |
 |

|  |