PhD thesis
"Mathematical modeling and numerical simulation
of innovative electronic nanostructures".
This thesis with joint supervision
(available here in PDF format) has been defended on November 25th 2011 in front of a jury involving:
| P. Degond |
(CNRS IMT Toulouse) |
supervisor, |
| L. Desvillettes |
(CMLA ENS Cachan) |
reviewer, |
| A. Jüngel |
(TU Wien) |
reviewer, |
| I. Perugia |
(DIMAT Pavia) |
member, |
| P. Pietra |
(IMATI-CNR Pavia) |
supervisor, |
| J.-M. Roquejoffre |
(IMT Toulouse) |
member. |
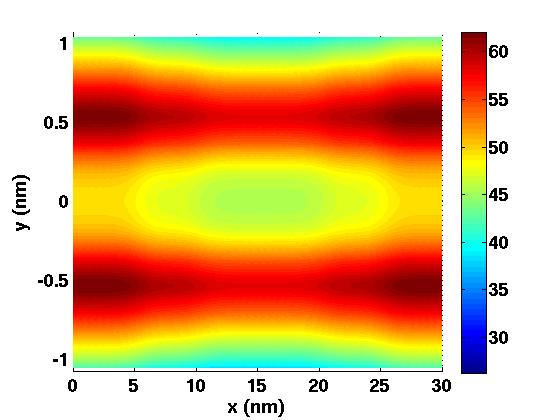
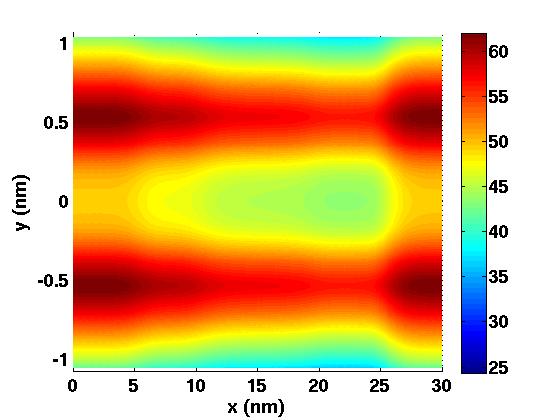
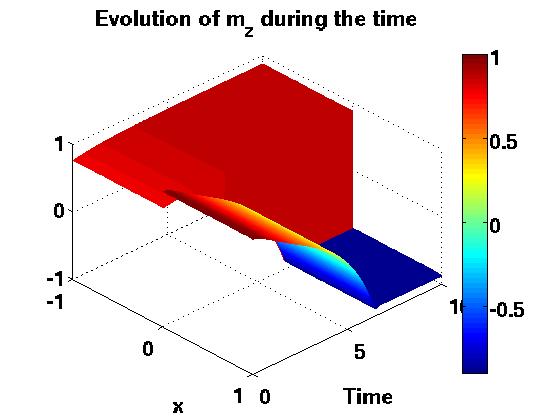
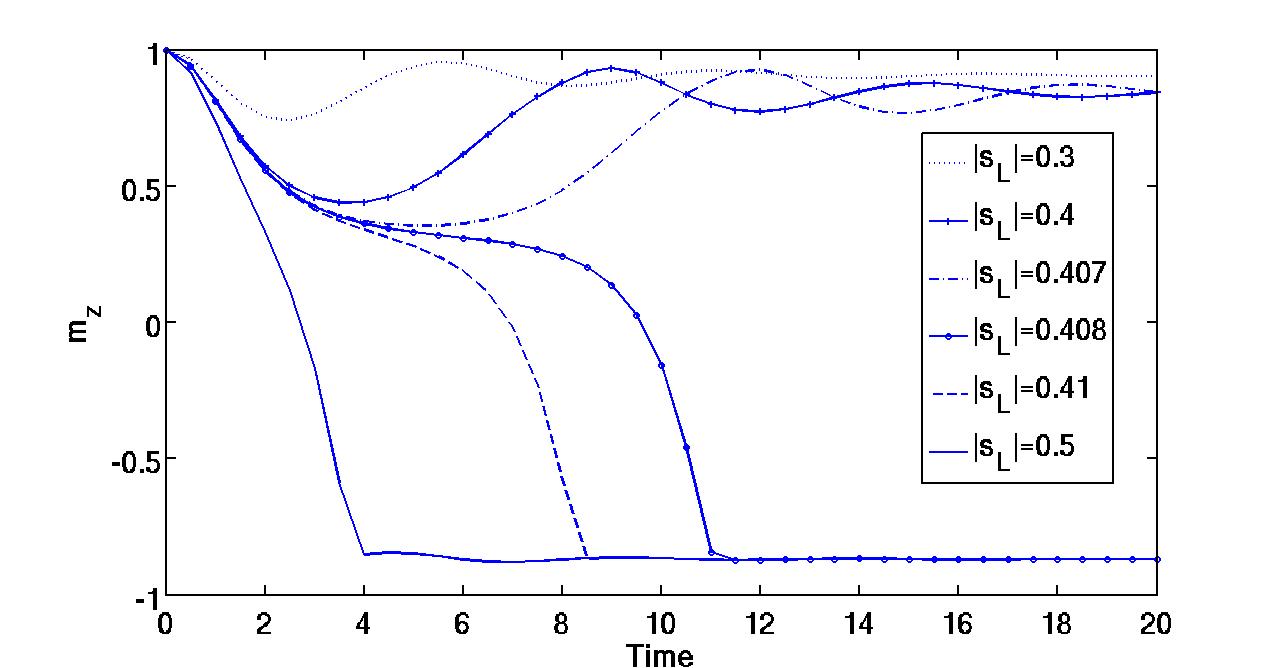
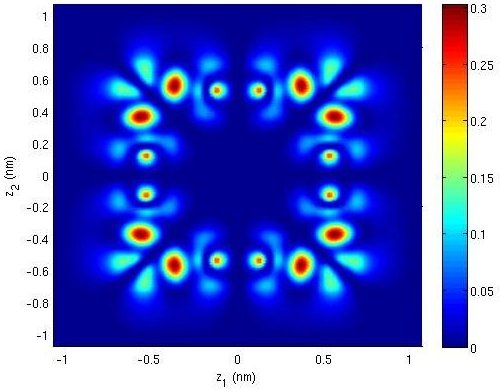
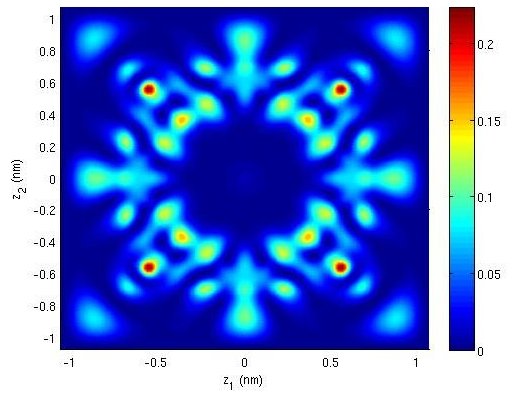
In this PhD thesis, we are interested in the modeling and the simulation of innovative electronic nanodevices. First, we formally derive an effective mass model describing the quantum motion of electrons in ultra-scaled confined nanostructures. Numerical simulations aim at testing the relevance of the obtained model for a simplified (but already significant) device. The second part is devoted to non-ballistic transport in these confined nanostructures. We rigorously analyse a drift-diffusion model and afterwards we describe and implement a classical-quantum spatial coupling approach. In the last part, we model and simulate a spintronic nanodevice. More precisely, we study the magnetization switching of a ferromagnetic material driven by a spin-current.
Keywords: ultra-scaled confined nanostructures, effective mass approximation, classical/quantum transport, Schrödinger-Poisson system, drift-diffusion equation, spintronics and spin transfer, Landau-Lifshitz equation, multiscale analysis, asymptotic expansions, high-performance computation.