L'assertion
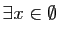 est fausse (par définition
l'ensemble vide ne contient aucun élément). Toute
implication qui commence par
est fausse (par définition
l'ensemble vide ne contient aucun élément). Toute
implication qui commence par
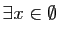 est forcément
vraie, par définition de l'implication. Il est donc indispensable,
avant de se lancer dans la démonstration d'une implication, de
vérifier que les hypothèses ne sont pas vides,
c'est-à-dire qu'elles sont
satisfaites par au moins un objet. Sans cela, on pourrait en déduire
tout et n'importe quoi. Par exemple l'assertion suivante est
mathématiquement correcte,
même si nous ne vous conseillons pas de l'apprendre par c
est forcément
vraie, par définition de l'implication. Il est donc indispensable,
avant de se lancer dans la démonstration d'une implication, de
vérifier que les hypothèses ne sont pas vides,
c'est-à-dire qu'elles sont
satisfaites par au moins un objet. Sans cela, on pourrait en déduire
tout et n'importe quoi. Par exemple l'assertion suivante est
mathématiquement correcte,
même si nous ne vous conseillons pas de l'apprendre par c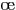 ur :
ur :
Soit
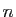
un entier tel que
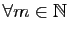
,
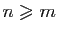
. Alors
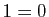
.
Proposition 14
Il existe deux nombres irrationnels 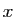 et
et 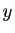 tels que
tels que 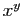 soit rationnel.
soit rationnel.
Démonstration : Nous avons vu que le nombre 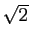 est irrationnel. Essayons
est irrationnel. Essayons
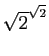 : il est soit rationnel, soit irrationnel.
: il est soit rationnel, soit irrationnel.
- Si
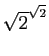 est rationnel, la proposition est
démontrée, puisque
est rationnel, la proposition est
démontrée, puisque
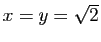 convient.
convient.
- Si
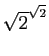 est irrationnel, posons
est irrationnel, posons
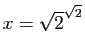 , et
, et
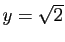 . Alors
. Alors
et la proposition est également démontrée.

Rien dans cette démonstration ne permet de savoir si
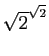 est ou non rationnel, et donc l'existence de
est ou non rationnel, et donc l'existence de
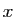 et
et 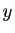 est démontrée sans qu'on puisse exhiber un seul
exemple. On dit que la démonstration est «non constructive».
est démontrée sans qu'on puisse exhiber un seul
exemple. On dit que la démonstration est «non constructive».
Certains mathématiciens, à la suite de Luitzen Brouwer
(1881-1966), affirment qu'il n'est pas acceptable de
démontrer un théorème d'existence sans
être capable de construire au moins un objet vérifiant la
propriété. Ils considèrent que cela revient à peu près à
affirmer que les licornes existent parce qu'on trouve la définition du
mot «licorne» dans les dictionnaires. À vous de juger...
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
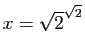 , et
, et
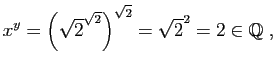
![]() est ou non rationnel, et donc l'existence de
est ou non rationnel, et donc l'existence de
![]() et
et ![]() est démontrée sans qu'on puisse exhiber un seul
exemple. On dit que la démonstration est «non constructive».
est démontrée sans qu'on puisse exhiber un seul
exemple. On dit que la démonstration est «non constructive».
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales