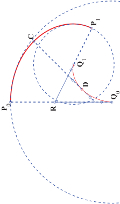
|
Pythagorean hodograph spline spirals that match G3 Hermite data from circles
Zhong Li, Rachid Ait-Haddou and Luc Biard
Journal of Computational and Applied Mathematics, 278, pp. 162-180, 2015
Abstract :
A construction is given for a G3 piecewise rational Pythagorean hodograph convex spiral
which interpolates two G3 Hermite data associated with two non-concentric circles, one
being inside the other. The spiral solution is of degree 7 and is the involute of a G2
convex curve, referred to as the evolute solution, with prescribed length, and composed
of two PH quartic curves. Conditions for G3 continuous contact with circles are then
studied and it turns out that an ordinary cusp at each end of the evolute solution is
required. Thus, geometric properties of a family of PH polynomial quartics, allowing to
generate such an ordinary cusp at one end, are studied. Finally, a constructive algorithm
is described with illustrative examples.
|

|
Surfaces reconstruction via inertial sensors for monitoring
Nathalie Saguin-Sprynski, Laurent Jouanet, Bernard Lacolle and Luc Biard
7th European Workshop on Structural Health Monitoring, pp. 702-709, 2014
Abstract :
This document deals with the new capabilities of monitoring via the surface
reconstruction of structures with sensors’ arrays systems. Indeed, we will
detail here our new demonstrator composed of a smart textile equipped with
inertial sensors and a set of processings allowing to reconstruct the shape
of the textile moving along time. We show here how this new tool can provide
very useful information from the structures.
|

|
C2 interpolation of spatial data subject to arc-length constraints using Pythagorean–hodograph quintic splines
Mathieu Huard, Rida T. Farouki, Nathalie Sprynski and Luc Biard
Graphical Models, 76, pp. 30-42, 2014
Abstract :
In order to reconstruct spatial curves from discrete electronic sensor data,
two alternative C2 Pythagorean–hodograph (PH) quintic spline formulations are
proposed, interpolating given spatial data subject to prescribed constraints
on the arc length of each spline segment.
The first approach is concerned with the interpolation of a sequence of points,
while the second addresses the interpolation of derivatives only (without spatial
localization). The special structure of PH curves allows the arc-length
conditions to be expressed as algebraic constraints on the curve coefficients.
The C2 PH quintic splines are thus defined through minimization of a quadratic
function subject to quadratic constraints, and a close starting approximation
to the desired solution is identified in order to facilitate efficient construction
by iterative methods. The C2 PH spline constructions are illustrated by several
computed examples.
|
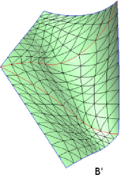
|
Reconstruction of quasi developable surfaces from ribbon curves
Mathieu Huard, Nathalie Sprynski, Nicolas Szafran and Luc Biard
Numerical Algorithm, 63, pp. 483-506, 2013
Abstract :
This paper deals with the acquisition and reconstruction of physical
surfaces by mean of a ribbon device equipped with micro-sensors, providing
geodesic curves running on the surface. The whole process involves the
reconstruction of these 3D ribbon curves together with their global treatment
so as to produce a consistent network for the geodesic surface interpolation
by filling methods based on triangular Coons-like approaches. However, the
ribbon curves follow their own way, subdividing thus the surface into arbitrary
n-sided patches. We present here a method for the reconstruction of quasi
developable surfaces from such n-sided curvilinear boundary curves acquired
with the ribbon device.
|
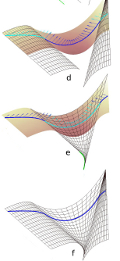
|
Rubans géodésiques pour la segmentation et la reconstruction de surfaces développables
Mathieu Huard, Nathalie Sprynski, Nicolas Szafran, Luc Biard
Journées du GTMG, Strasbourg, Mars 2012
Abstract :
This paper deals with the acquisition and reconstruction of physical developable
G1 surfaces by using a ribbon equipped with micro-accelerometers and
micro-magnetometers, providing geodesic curves running on the surface.
The method consists in working with the space of tangent planes provided
by the geodesics, where the different components of the surface can be
identified, and then reconstructed as beams of lines going through the
acquired geodesics.
|
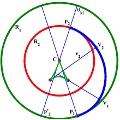
|
On the interpolation of concentric curvature elements
Carlotta Giannelli and Luc Biard
Computer-Aided Design, Volume 43, Issue 6, pp. 586-597, June 2011
Abstract :
A convex G2 Hermite interpolation problem of concentric curvature elements is considered in this paper.
It is first proved that there is no spiral arc solution with turning angle less than or equal to $\pi$ and then,
that any convex solution admits at least two vertices. The curvature and the evolute profiles of such
an interpolant are analyzed. In particular, conditions for the existence of a G2 convex interpolant with
prescribed extremal curvatures are given.
|

|
Motion Capture of an Animated Surface via Sensors Ribbons
Nathalie Sprynski, Bernard Lacolle and Luc Biard
In Proceeding of the First International Conference on Pervasive and Embedded Computing and Communication Systems,
Vilamoura, Algarve, Portugal, 5-7 March, 2011
Abstract :
This paper deals with the motion capture of physical surfaces via a curve acquisition device.
This device is a ribbon of sensors, named Ribbon Device, providing tangential measurements,
allowing to reconstruct its 3D shape via an existing geometric method. We focus here on the
problem of reconstructing animated surfaces, from a finite number of curves running on these surfaces,
acquired with the Ribbon Device. This network of spatial curves is organized according a comb
structure allowing to adjust these curves with respect to a reference curve, and then to develop
a global C1 reconstruction method based on the mesh of ribbon curves together with interpolating
transversal curves. Precisely, at each time position the surface is computed from the previous step
by an updating process.
|
|
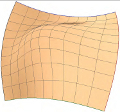
A Construction of rational surface patches bounded by lines of curvature
Luc Biard, Rida T. Farouki, Nicolas Szafran
Computer Aided Geometric Design, Volume 27(5), pp. 359--371, 2010
Abstract :
The fact that the Darboux frame is rotation--minimizing along lines of
curvature of a smooth surface is invoked to construct rational surface
patches whose boundary curves are lines of curvature. For given patch
corner points and associated frames defining the surface normals and
principal directions, the patch boundaries are constructed as quintic RRMF
curves, i.e., spatial Pythagorean--hodograph (PH) curves that possess
rational rotation--minimizing frames. The interior of the patch is then
defined as a Coons interpolant, matching the boundary curves and their
associated rotation--minimizing frames as surface Darboux frames. The
surface patches are compatible with the standard rational B\'ezier/B--spline
representations, and $G^1$ continuity between adjacent patches is easily
achieved. Such patches are advantageous in surface design with more
precise control over the surface curvature properties.
|
|
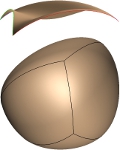
Construction and smoothing of triangular Coons patches with geodesic boundary curves
Rida T. Farouki, Nicolas Szafran, Luc Biard
Computer Aided Geometric Design, Volume 27(4), pp. 301--312, 2010
Abstract :
Given three regular space curves ${\bf r}_1(t)$, ${\bf r}_2(t)$,
${\bf r}_3(t)$ for $t\in[\,0,1\,]$ that define a curvilinear triangle,
we consider the problem of constructing a triangular surface
patch ${\bf R}(u_1,u_2,u_3)$ bounded by these three curves, such
that they are geodesics of the constructed surface. Results from a
prior study \citep{Farouki09} concerned with tensor--product patches
are adapted to identify constraints on the given curves for the
existence of such geodesic--bounded triangular surface patches.
For curves satisfying these conditions, the patch is constructed
by means of a cubically--blended triangular Coons interpolation
scheme. A formulation of thin--plate spline energy in terms of
barycentric coordinates with respect to a general domain triangle
is also derived, and used to optimize the smoothness of the
geodesic--bounded triangular surface patches.
|
|
A Refinement of the Variation Diminishing Property of Bézier Curves
Rachid Ait-Haddou, Taishin Nomura and Luc Biard
Computer Aided Geometric Design, Volume 27, Issue 2, Pages 202-211, February 2010
Abstract :
For a given polynomial $F(t)= \sum_{i=0}^{n} p_i B_i^n(t)$,
expressed in the Bernstein basis over an interval $[a,b]$,
we prove that the number of real roots of $F(t)$ in $[a,b]$,
counting multiplicities, does not exceed the sum of
the number of real roots in $[a,b]$ of the polynomial
$G(t)= \sum_{i=k}^l p_i B_{i-k}^{l-k}(t)$
(counting multiplicities)
with the number of sign changes in the two sequences
$(p_0,...,p_k)$ and $(p_l,...,p_n)$
for any value $k,l$ with $0\leq k \leq l \leq n$.
As a by product of this result, we give
new refinements of the classical variation diminishing
property of B\'ezier curves.
|

|
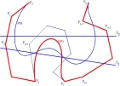
Construction of Bézier surface patches with Bézier curves as geodesic boundaries
Rida T. Farouki, Nicolas Szafran, Luc Biard
Computer Aided Design, Vol. 41, pp. 772--781, 2009
Abstract :
Given four polynomial or rational B\'ezier curves defining a curvilinear
rectangle, we consider the problem of constructing polynomial or rational
tensor--product B\'ezier patches bounded by these curves, such that they
are geodesics of the constructed surface. The existence conditions and
interpolation scheme, developed in a general context in earlier studies,
are adapted herein to ensure that the geodesic--bounded surface patches
are compatible with the usual polynomial/rational representation schemes
of CAD systems. Precise conditions for four B\'ezier curves to constitute
geodesic boundaries of a polynomial or rational surface patch are identified,
and an interpolation scheme for the construction of such surfaces is
presented when these conditions are satisfied. The method is illustrated
with several computed examples.
|

|
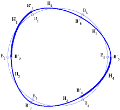
Existence conditions for Coons patches interpolating geodesic boundary curves
Rida T. Farouki, Nicolas Szafran, Luc Biard
Computer Aided Geometric Design, Volume 26, Issue 5, pp. 599-614, June 2009
Abstract :
Given two pairs of regular space curves ${\bf r}_1(u)$, ${\bf r}_3(u)$
and ${\bf r}_2(v)$, ${\bf r}_4(v)$ that define a curvilinear rectangle,
we consider the problem of constructing a $C^2$ surface patch ${\bf R}
(u,v)$ for which these four boundary curves correspond to geodesics of the
surface. The possibility of constructing such a surface patch is shown to
depend on the given boundary curves satisfying two types of consistency
constraints. The first constraint is global in nature, and is concerned
with compatibility of the variation of the principal normals along the
four curves with the normal to an oriented surface. The second constraint
is a local differential condition, relating the curvatures and torsions of
the curves meeting at each of the four patch corners to the angle between
those curves. For curves satisfying these constraints, the surface patch
is constructed using a bicubically--blended Coons interpolation process.
|
|
Pythagorean-hodograph ovals of constant width
Ait-Haddou Rachid, Walter Herzog and Luc Biard
Computer Aided Geometric Design, Volume 25, 4-5, pp. 258--273, May 2008
Abstract :
A constructive geometric approach to rational ovals and rosettes
of constant width formed by piecewise rational PH curves is presented.
We propose two main constructions. The first construction, models with rational PH curves
of algebraic class $3$ (T-quartics) and is based on the fact that T-quartics are
exactly the involutes of T-cubic curves. The second construction, models with rational
PH curves of algebraic class $m > 4$ and is based on the dual control structure of offsets
of rational PH curves.
|

|
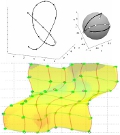
Surface reconstruction via geodesic interpolation
Nathalie Sprynski, Nicolas Szafran, Bernard Lacolle and Luc Biard
Computer-Aided Design, Volume 40, Issue 4, pp. 480-492, April 2008
Abstract :
This paper is concerned with reconstruction of numerical or real surfaces
based on the knowledge of some geodesic curves on the surface.
So, considering two regular 3D-curves $f_0(t)$ and $f_1(t)$,
our purpose is to construct a surface which interpolates these two curves in such a way
that these two curves are geodesics on this surface.
This will be accomplished using Hermite interpolation.
For a real surface, it will be shown that geodesics can be acquired
using a ribbon of micro-sensors.
|
|
Curve and Surface Reconstruction via Tangential Information
Nathalie Sprynski, Bernard Lacolle, Dominique David and Luc Biard
Curve and Surface Design : Avignon 2006, P. Chenin, T. Lyche, L. L. Schumaker (eds),
Nashboro Press, pp. 254--263, 2007
Abstract :
This paper presents a novel method for recontructing surfaces
relying only on tangential data which are provided by embedded
sensors. The reconstruction process is based on the knowledge of the
distribution of the sensors, which are organized as a square mesh,
and on the associated tangential orientation measurements without
any information about their positioning in space so that this problem
cannot be solved by envelope methods. We provide methods for planar
and spatial curves, then extend them for surfaces. We validate
these methods proving their convergence and by the analysis of the
results obtained in a physical point of view. Finally, we show the
implementation of our work in a real time prototype.
|

|
Curve Reconstruction via a Ribbon of Sensors
Nathalie Sprynski, Bernard Lacolle, Dominique David and Luc Biard
In Proceeding of the 14th IEEE International Conference on Electronics, Circuits and Systems,
ICECS - 2007, December 2007
Abstract :
This paper presents a novel method for reconstructing curves relying on tangential data
which are provided by embedded sensors. The reconstruction process is based on the
knowledge of the distribution of the sensors along the curve, represented by a ribbon,
and on the associated tangential orientation measurements without any information
about their positioning in space, so that this problem is not an envelope problem.
We first show how we can obtain these data from sensors and the prototypes we
have created. Then we provide methods for planar curves, then for spatial curves
and we analyze results with physical sense and convergence in order to validate
these methods. Finally, we show some results from both simulated data and real data.
|

 Contact
Contact
















