| Home | Gallery | CV | Visit | Publications |
Regularity of optimal transport on oblate ellipsoids
in collaboration with Q. Mérigot
The question of regularity of optimal transport plans has received a lot of attention. Examples of discontinuous transport plans have been found by Caffarelli, between probability densities on the plane with non-convex support, and by Loeper on compact manifolds with negative curvature even for densities lower bounded by a positive constant (see e.g. Chapter 12 of the book of C. Villani). An even more striking recent result is that even on simple convex surfaces, it is possible to find examples of pairs of non-vanishing probability densities such that the optimal transport map is discontinuous (see recent papers of [B. Bonnard,J.B. Caillau,L. Rifford] and [A. Figalli,L. Rifford,C. Villani]). We study below numerically by our optimization method the case of oblate ellipsoids, which is one of the simplest cases where discontinuity can occur. More details can be found in our paper Discrete optimal transport: complexity, geometry and applications.
The family of ellipsoids 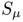 we will consider is defined by
we will consider is defined by 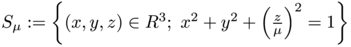 Bonnard, Caillau and Rifford have shown that for
Bonnard, Caillau and Rifford have shown that for 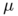 smaller than
smaller than 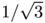 , there exists a point on the equator
, there exists a point on the equator 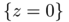 whose injectivity domain is non-convex. This fact implies the existence of two absolutely continuous probability measure
whose injectivity domain is non-convex. This fact implies the existence of two absolutely continuous probability measure 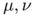 with densities in
with densities in ![$[C^{-1}, C]$](form_6.png) such that the optimal transport plan between
such that the optimal transport plan between 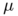 and
and 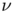 is discontinuous.
is discontinuous.
 |
 |
 |
 |
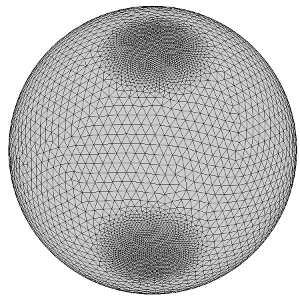
To obtain a qualitative description of this phenomena, we introduce two non-vanishing densities with equal total mass on  , whose formula in Cartesian coordinates is given by:
, whose formula in Cartesian coordinates is given by:
![\[ f(x,y,z)= 0.05+4\exp\left(-c(1-x)^2\right) \]](form_10.png)
and
![\[ g(x,y,z)= 0.05+2\exp\left(-c(1-\frac{\sqrt{2}}{2}(z+y))^2\right) + 2\exp\left(-c(1-\frac{\sqrt{2}}{2}(z-y))^2\right) \]](form_11.png)
with  . Previous parameters have been selected to define non-vanishing densities which are not too concentrated. Even in this regular situation, we will see that optimal transport maps may have very different qualitative behaviors depending on the eccentricity of the ellipsoid.
. Previous parameters have been selected to define non-vanishing densities which are not too concentrated. Even in this regular situation, we will see that optimal transport maps may have very different qualitative behaviors depending on the eccentricity of the ellipsoid.
We construct a quantization by a sum of 10000 unit Dirac masses of the two measures of densities  and
and 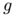 with respect to the two dimensional Hausdorff measure on $S_1$ using Lloyd's algorithm. Our goal is to compare here the optimal transport between the two discrete measures on the sphere and between two analogous measures defined on the oblate ellipsoid
with respect to the two dimensional Hausdorff measure on $S_1$ using Lloyd's algorithm. Our goal is to compare here the optimal transport between the two discrete measures on the sphere and between two analogous measures defined on the oblate ellipsoid 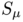 , with
, with 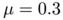 . By analogous we mean that we deduce our two measures on
. By analogous we mean that we deduce our two measures on 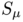 by the naive bi-Lipschitz transformation
by the naive bi-Lipschitz transformation
![\[(x,y,z)\rightarrow (x,y,\mu z).\]](form_17.png)
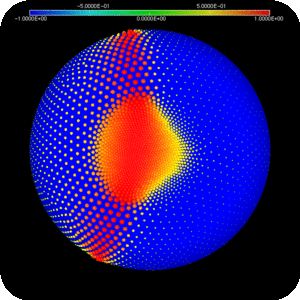
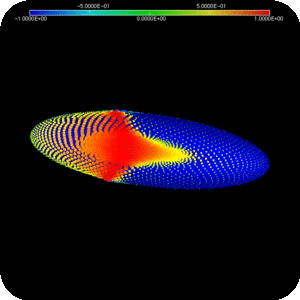
To illustrate the difference between the two optimal transports, we computed for every sampling point of the source densities the geodesic distance between its image and the center of the Gaussian part of the source density, i.e. the point 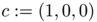 . More formally, this is equivalent to compute the pullback of the geodesic distance function to
. More formally, this is equivalent to compute the pullback of the geodesic distance function to 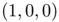 by the optimal transport. These functions are rescaled to have the same infinity norm, and their values are reported in the following figures, with the same color map. One can observe that the function is smooth along the equator in the spherical case (
by the optimal transport. These functions are rescaled to have the same infinity norm, and their values are reported in the following figures, with the same color map. One can observe that the function is smooth along the equator in the spherical case ( 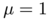 ) whereas in the oblate case (
) whereas in the oblate case ( 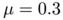 ) some points close to the equator can be transported to points whose geodesic distance to
) some points close to the equator can be transported to points whose geodesic distance to 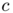 is very different. This qualitative behavior, observed here at a discrete level, is the first numerical illustration of the discontinuity of optimal transport plans between two non-vanishing densities supported on a convex manifold.
is very different. This qualitative behavior, observed here at a discrete level, is the first numerical illustration of the discontinuity of optimal transport plans between two non-vanishing densities supported on a convex manifold.
 |
 |
Move your mouse on the pictures to animate (slow connection be patient)
 |
 |