| Home | Gallery | CV | Visit | Publications |
Mass transportation with congested dynamics
in collaboration with G. Buttazzo and C. Jimenez
Here are some results obtained in collaboration with Guiseppe Buttazzo and Chloé Jimenez. All details can be found in our paper "Mass transportation with congested dynamics" (see also the publication section).
Mass transportation theory received much attention in the mathematical community in the last years. Starting from the initial setting by Monge where, given two mass densities ρ0(x) and ρ1(x), a transport map T: Rd→ Rd was searched among the admissible maps transporting ρ0 onto ρ1 in order to minimize the total transportation cost.
Several other equivalent formulations have been provided. The dynamic formulation given by Benamou and Brenier is the one which motivated our study: the goal was to introduce a “dynamic” formulation of the mass transportation problem providing a map ρ:[0,1]→ P(Ω) which describes the motion of ρ0 onto ρ1 as a function of a parameter t∈[0,1], where Ω is the space constraint that all the densities ρ(t,⋅) have to fulfill.
Very often concrete cases are related to the Wasserstein distances Wp(ρ0,ρ1), where each particle x in the source ρ0 moves to its final point T(x) in the target ρ1 following a line segment, or a geodesic line in case the space constraint Ω is not convex. However, in many problems where a high number of particles (or a probability density) is involved, other effects are present which may deviate the trajectories from straight lines: in particular we are interested in the congestion effects that occur when the density ρ(t,x) is high, slowing the ideal mass transportation and increasing the cost.
 |
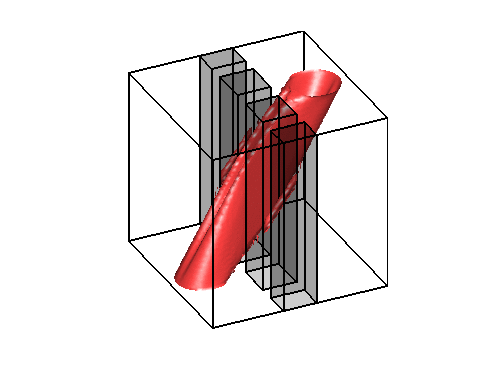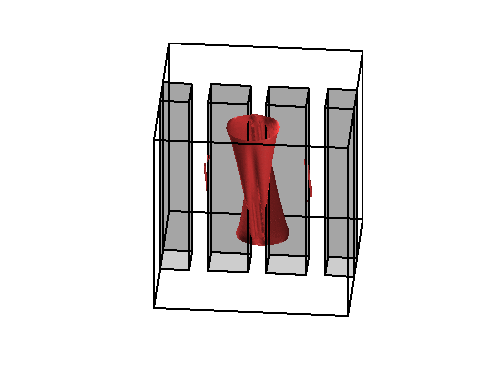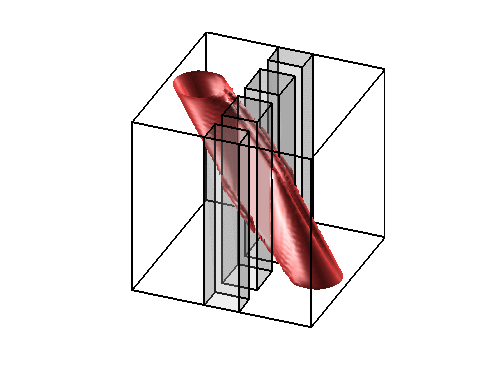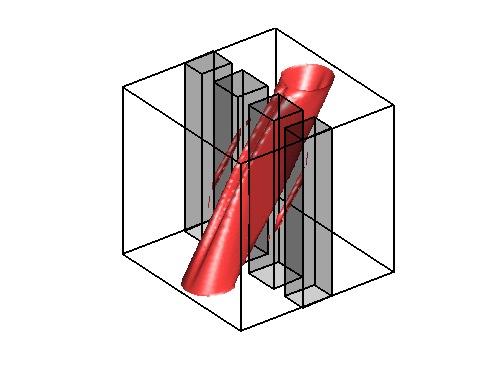 |
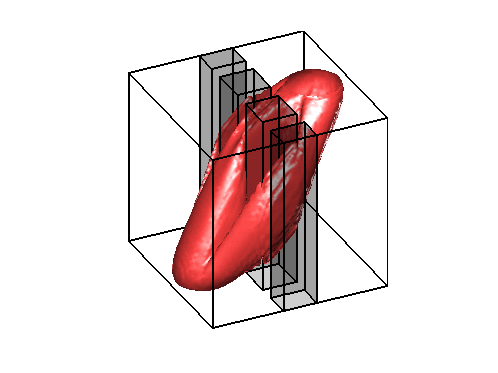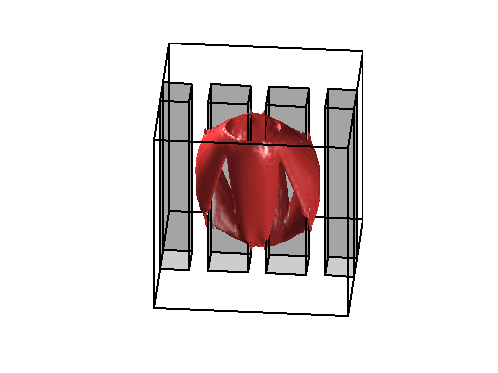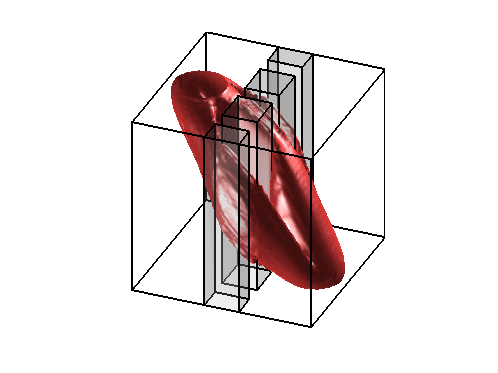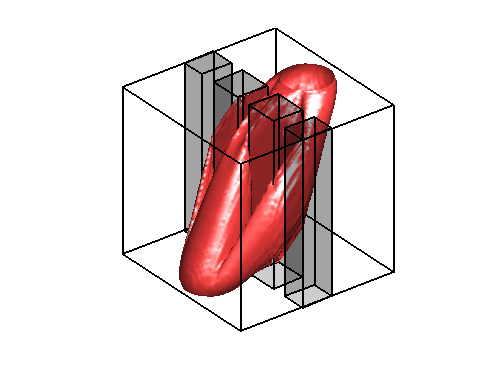
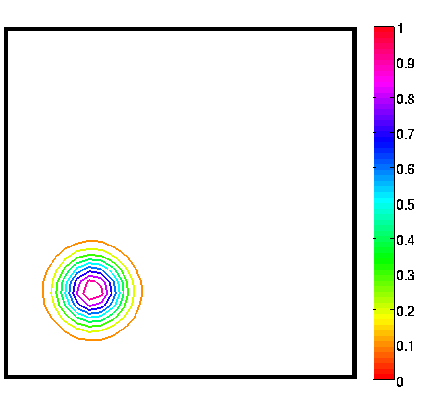
Level sets 0.1 of the two density functions corresponding to the situations described below on the right.
Modelling the congestion effects has been considered by several authors (see for instance the recent articles of Maury, Carlier, Jimenez, Santambrogio). In this work we simply consider the Benamou-Brenier formulation assuming that the functional has a term which has a superlinear growth with respect to ρ.
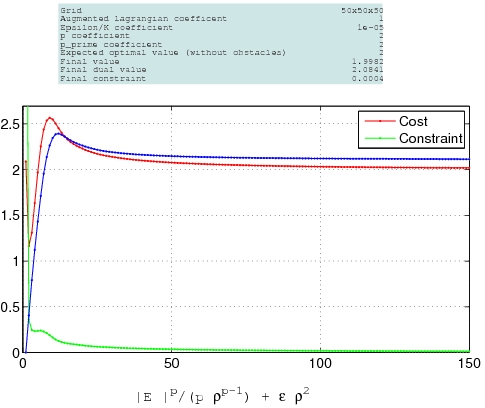
We present below some of our result related to our modelisation of the congestion effect. Those simulations have been carried out using the very performing software freeFEM3D developped by Stéphane Del Pino .
Move your mouse on the left picture to see the evolution (slow connection be patient)
|
|
A simple test case : the optimal transport path for the Wasserstein distance
2 between two identical Gaussian densities (the solution is obviously the translation)
Move your mouse on the pictures to animate (slow connection be patient)
 |
 |
 |
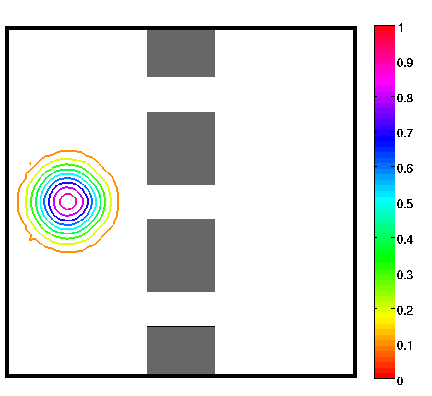
On the left, the same test case as above with obstacles (observe that the evolution of
the density is contained in the geodesic envelopp of the densities as expected).
The two pictures on the right illustrate the congestion effect.
In the middle a diffusion term proportionnal to the square of the density has been added to the cost functionnal.
On the right, a bound equal to 1 has been imposed to the density.
 |
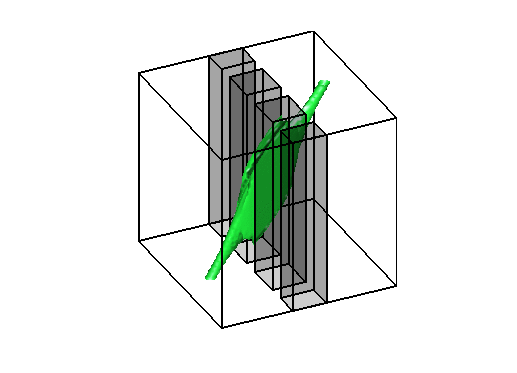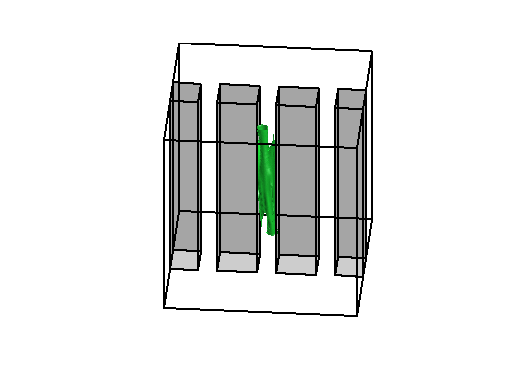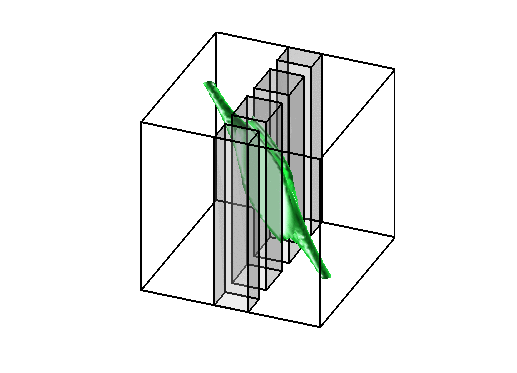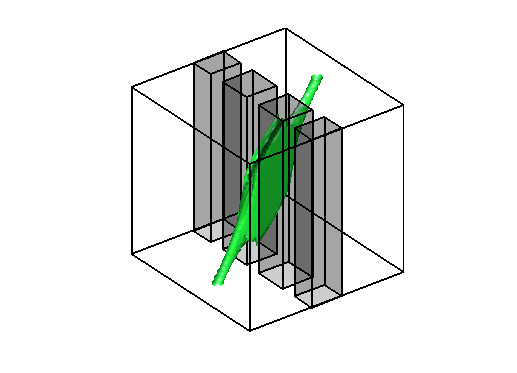 |
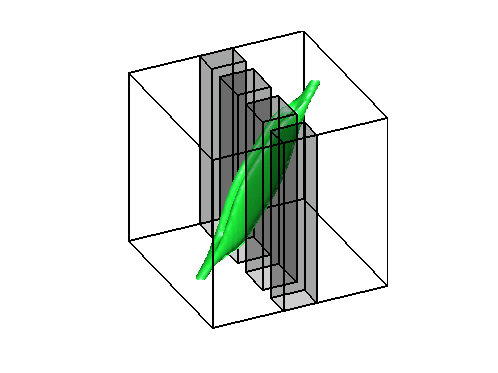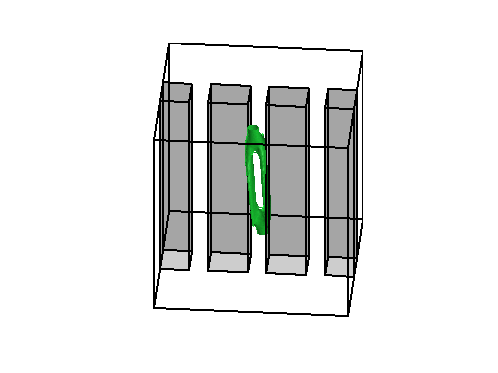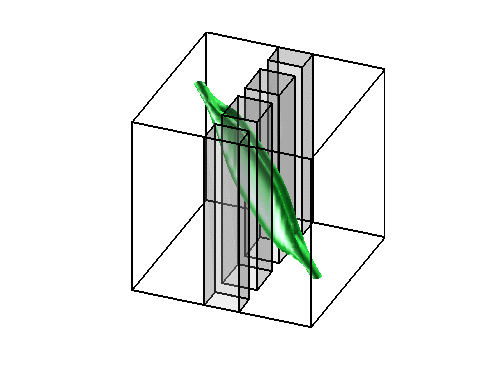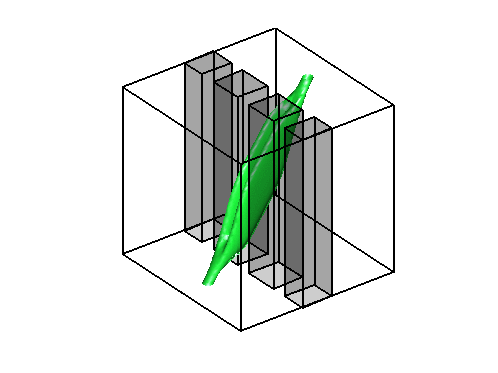
Level sets 0.9 of the two density functions corresponding to the situations
described above on the right. Notice that high density is only located along the edges of the obstacles
without the bound constraint and not in the middle of the channel.