| Home | Gallery | CV | Visit | Publications |
Reconstruction of a convex body from its Gaussian curvature measure
in collaboration with Q. Mérigot
We describe below a method to reconstruct a 3D convex body from its Gaussian curvature measure based on a variational characterization based on optimal transport due to [V. Oliker (2007) and J. Bertrand (2010)]. All details can be found in our paper Discrete optimal transport: complexity, geometry and applications.
Let  be a convex body in
be a convex body in 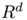 , containing the origin in its interior. Any convex set admits an exterior unit normal vector field
, containing the origin in its interior. Any convex set admits an exterior unit normal vector field 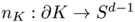 , which is uniquely defined almost everywhere. Let
, which is uniquely defined almost everywhere. Let 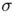 be the probability measure on the unit sphere, obtained by rescaling the
be the probability measure on the unit sphere, obtained by rescaling the 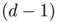 -dimensional Hausdorff measure. The Gaussian measure
-dimensional Hausdorff measure. The Gaussian measure 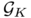 of
of 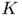 is by definition the pullback of
is by definition the pullback of 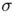 by the Gauss map
by the Gauss map 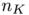 . More explicitly,
. More explicitly,
![\[ \forall B \subseteq \partial K,~ \mathcal{G}_K(B) := \sigma(n_K(B))\]](form_8.png)
Since 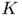 contains the origin in its interior, its boundary can be parameterized by a radial map
contains the origin in its interior, its boundary can be parameterized by a radial map 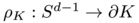 . For every direction
. For every direction 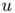 in
in 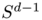 ,
, 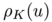 lies in the intersection of
lies in the intersection of 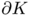 with the ray
with the ray 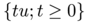 . We can again pull-back the measure
. We can again pull-back the measure 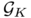 by the map
by the map 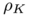 , thus defining a measure on the unit sphere
, thus defining a measure on the unit sphere 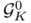 , which we will call Alexandrov measure.
, which we will call Alexandrov measure.
![\[ \forall B \subseteq S^{d-1},~ \mathcal{G}^0_K(B) := \sigma(n_K\circ \rho_K(B)).\]](form_17.png)
Move your mouse on the pictures to animate
 |
 |
Alexandrov addressed the question of the existence and uniqueness (up to homotethy) of a convex body with prescribed Alexandrov measure 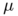 , under some conditions on
, under some conditions on 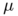 . The relationship between this reconstruction problem and a problem of optimal transport on the unit sphere for the cost
. The relationship between this reconstruction problem and a problem of optimal transport on the unit sphere for the cost 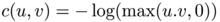 has been first remarked by Oliker, and then used by Bertrand to give a direct variational proof of Alexandrov theorem. Bertrand's version of Alexandrov's theorem says the following:
has been first remarked by Oliker, and then used by Bertrand to give a direct variational proof of Alexandrov theorem. Bertrand's version of Alexandrov's theorem says the following:
 Given a probability measure
Given a probability measure  on the unit sphere, there exists a convex body
on the unit sphere, there exists a convex body  such that
such that 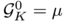 if and only the following optimal transport problem between
if and only the following optimal transport problem between 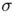 and
and 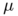 for the cost function
for the cost function 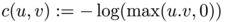 admits a solution with finite cost:
admits a solution with finite cost:
![\[ \sup_{\phi,\psi} \int_{S^{d-1}} \phi(u)\, d\sigma - \int_{S^{d-1}}\psi(v)\, d\mu = \inf_{\pi} \int_{S^{d-1} \times S^{d-1}} c(u,v) \\, d \pi(u,v) \]](form_23.png)
where the maximum is taken over functions 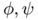 satisfying the relation
satisfying the relation 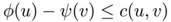 , and the infimum is taken over transport plans between
, and the infimum is taken over transport plans between 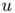 and
and 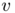 .
.
Based on this observation we solve previous non-standard optimal transportation problem to reconstruct convex bodies from their Gauss measures.
Move your mouse on the pictures to animate
 |
 |