| Home | Gallery | CV | Visit | Publications |
Spectral optimization with ShapeBox : the (new) pinched ball conjecture
in collaboration G. Vial
The ShapeBox project
ShapeBox is a new web interface which allows you to investigate 2D optimization problems related to shape functionals (3D will be available in the next release). Your query is submitted online, launching the computation dynamically on our server. Once the job is done, you receive an email with a link to the result webpage. Due to the problems which have motivated its development, ShapeBox is first dedicated to spectral optimization. The objective function may be any algebraic quantity depending on Laplace-Dirichlet, Laplace-Neumman or Laplace-Beltrami eigenfunctions and other geometrical quantities.
Such optimization problems raise serious numerical difficulties. First the number of connected components of an optimal shape and their topologies are not prescribed. Additionally, even the simplest functionals have a large number of local minima. Last but not least, it is well known that in the case of multiple eigenvalues cost functionnals are not differentiable anymore. ShapeBox is designed to tackle those difficulties with the most recent techniques and also to develop new ones! In further developments, we plan to study optimization problems related to the solution of linear PDE's like elasticity, Stokes equation, Maxwell equations, etc.
Up to now, ShapeBox does not aim at solving real-life problems but gives the opportunity to test model optimization objective functions, under several constraint sets. In a first step, the resolution relies on a stochastic algorithm which gives a reasonable but not sharp approximation of (one of) the optimal shape(s). Next, this rough approximation is improved using a new local optimization method which will be described in a forthcoming paper.
ShapeBox is totally free. The procedure being automatic, no mathematical study is carried out and the results are given without any warranty. You can find additional information on the F.A.Q. page of ShapeBox or on the Solver page dedicated to the definition of your spectral problem (and its constraints). We give below a first flavor of what ShapeBox can produce.
Move your mouse on the pictures to animate (slow connection be patient)
 |
 |
The new pinched ball conjecture
The simplest shape optimization problem related to spectral quantities is perhaps the minimization of one eigenvalue under measure constraint. Namely :
![\[ \min_{|\Omega|=c} \lambda_k(\Omega) \]](form_0.png)
where 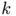 is a fixed integer,
is a fixed integer, 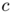 a given non negative constant,
a given non negative constant, 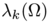 stands for the kth eigenvalue of the Laplace operator with Dirichlet conditions and
stands for the kth eigenvalue of the Laplace operator with Dirichlet conditions and 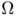 is a (measurable) subset of
is a (measurable) subset of 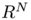 . In 1923, G. Faber and E. Krahn solved that problem for any
. In 1923, G. Faber and E. Krahn solved that problem for any 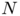 when
when 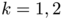 (see for instance [G. Faber, Beweis, dass unter allen homogenen Membranen von gleicher Flache a und gleicher Spannung die kreisformige den tiefsten Grundton gibt , Sitz. Ber. o Bayer. Akad. Wiss. (1923), 169-172]). As a matter of fact, by symmetrization techniques which are quite standard today, it is straightforward to prove that any ball of volume
(see for instance [G. Faber, Beweis, dass unter allen homogenen Membranen von gleicher Flache a und gleicher Spannung die kreisformige den tiefsten Grundton gibt , Sitz. Ber. o Bayer. Akad. Wiss. (1923), 169-172]). As a matter of fact, by symmetrization techniques which are quite standard today, it is straightforward to prove that any ball of volume 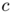 minimizes
minimizes 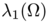 among sets of same volume. This is equivalent to the so called Faber-Krahn inequality:
among sets of same volume. This is equivalent to the so called Faber-Krahn inequality:
![\[ \lambda_1(\Omega) \geq \left(\frac{1}{|\Omega|}\right) ^{1/N} C^{2/N}_N j_{N/2-1,1} \]](form_9.png)
where 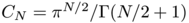 and
and 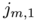 is the first positive zero of the Bessel function
is the first positive zero of the Bessel function 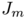 .
.
Move your mouse on the pictures of the second row to animate (be patient...)
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
By simple arguments related to the nodal components of the second eigenfunction they also proved, a few years later, that 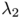 is minimized by the union of two identical disconnected balls of
is minimized by the union of two identical disconnected balls of 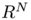 . Whereas a good analytical framework to obtain the existence of optimal shapes has been developed by G. Buttazzo and G. Dal Maso Buttazzo in 1993 (see [Giuseppe; Dal Maso, Gianni An existence result for a class of shape optimization problems. Arch. Rational Mech. Anal. 122 (1993), no. 2, 183–195.]), very few progresses have been done to deduce qualitative information related to optimal shapes for
. Whereas a good analytical framework to obtain the existence of optimal shapes has been developed by G. Buttazzo and G. Dal Maso Buttazzo in 1993 (see [Giuseppe; Dal Maso, Gianni An existence result for a class of shape optimization problems. Arch. Rational Mech. Anal. 122 (1993), no. 2, 183–195.]), very few progresses have been done to deduce qualitative information related to optimal shapes for 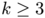 , even in dimension 2 !
, even in dimension 2 !
A first study has been carried out in Numerical Minimization of eigenmodes of a membrane with respect to the domain in 2D to obtain a numerical description of optimal shapes associated to 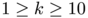 . We reproduce with ShapeBox those experiments to obtain the minimizers of
. We reproduce with ShapeBox those experiments to obtain the minimizers of 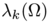 for
for 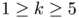 . Our results are displayed in the above pictures. As expected for
. Our results are displayed in the above pictures. As expected for 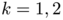 the disk and the union of two disk are found by ShapeBox. Moreover, as it is conjectured by most of the specialists, the disk is the expected minimizer of
the disk and the union of two disk are found by ShapeBox. Moreover, as it is conjectured by most of the specialists, the disk is the expected minimizer of 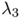 . Observe that for
. Observe that for 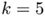 , the optimal shape is not anymore a union of disks.
, the optimal shape is not anymore a union of disks.
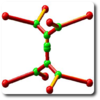
Using the flexibility of ShapeBox, we carried out the same experiments in 3D. Again, the already proved results for 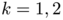 are found (see below). For
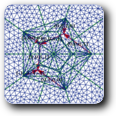
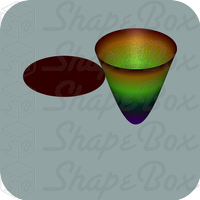
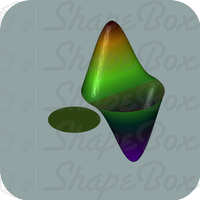
are found (see below). For 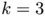 A. Henrot and D. Bucur proved that the optimal shape has to be connected. Considering the analogous situation in 2D, it is very natural to expect that the ball is also optimal in 3D . Surprisingly, this fact is contradicted by the result of ShapeBox (see the first picture of that page). More precisely, our computation gives:
A. Henrot and D. Bucur proved that the optimal shape has to be connected. Considering the analogous situation in 2D, it is very natural to expect that the ball is also optimal in 3D . Surprisingly, this fact is contradicted by the result of ShapeBox (see the first picture of that page). More precisely, our computation gives:
![\[ \lambda_3(B)|B|^{2/3} = j_{3/2,1}^2|B|^{2/3} \simeq 52.4656 > 49.1629562 > \lambda_3(P)|P|^{2/3} \]](form_21.png)
where 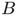 is a ball and
is a ball and 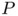 our "numerical pinched ball". Notice that the numerical computation of eigenmodes by finite element methods leads to upper bounds of the eigenvalues since the discrete computation is done on a space which is strictly included in
our "numerical pinched ball". Notice that the numerical computation of eigenmodes by finite element methods leads to upper bounds of the eigenvalues since the discrete computation is done on a space which is strictly included in 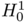 . Thus, we propose the following conjecture:
. Thus, we propose the following conjecture:
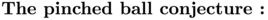
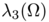 is not minimized among sets of constant measure by the ball in dimension 3 .
is not minimized among sets of constant measure by the ball in dimension 3 .
We give above three different discretization of our pinched ball. Based on these meshes, you can perform your own computation with your best eigensolver and your favorite finite element 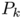 . please let us know if you can improve the previous bound. We will report any progress on this page.
. please let us know if you can improve the previous bound. We will report any progress on this page.
Move your mouse on the pictures to animate (be patient...)
 |
 |
 |
 |
 |
 |