| Home | Gallery | CV | Visit | Publications |
Optimal cutting of a bounded doamin into peaces of equal volume
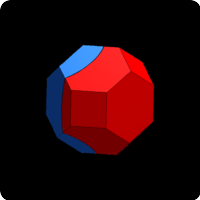
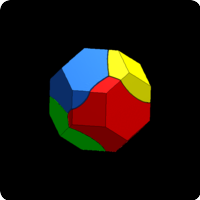
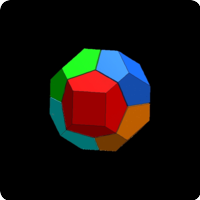
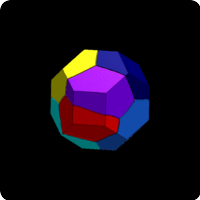
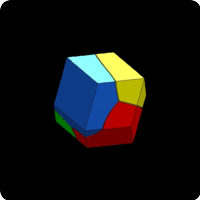
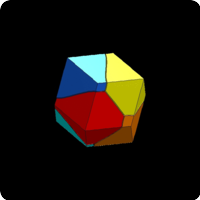
We study in this work the problem of dividing a bounded region of the plane/space into pieces of equal area/volume such as to minimise the length/surface of the boundary of the partition. This work follows a numerical study of Kelvin's conjecture which has been illustrated on the previous link. We present below some optimal cuttings obtained by a similar approach based on Γ-convergence which makes it possible to avoid many local minima. As a post treatment, we used the very efficient software Evolver (developped by Kennet A. Brakke) to obtain a finer description of optimal cuttings.
Click on a picture to see an animated view
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Optimal cuttings of polytopes obtained by gamma Γ-convergence
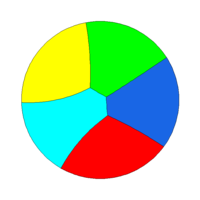
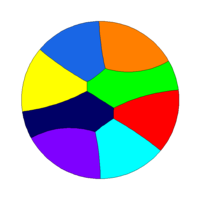
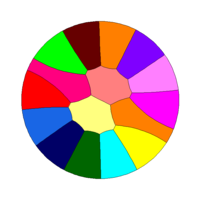
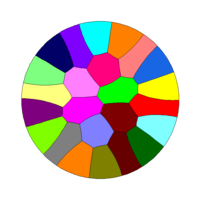
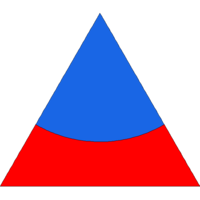
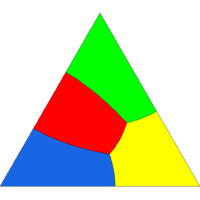
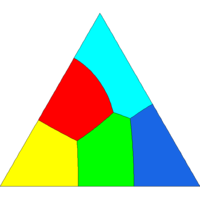
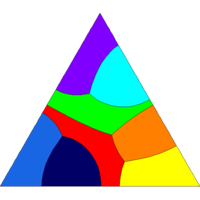
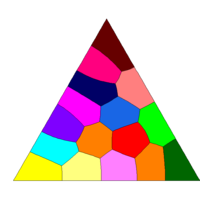
As test cases we give also some illustrations related to optimal partitions of the disc and of a triangle. As expected, our numerical solutions are made of local patches satisfying the 120 degrees angular conditions. Moreover some symmetries of the cutted set are preserved for small numbers of cells.
 |
 |
 |
 |
 |
 |
 |
 |
Tiling of a disk with 2, 3, 4, 5, 8, 16, 24, 32 cells
 |
 |
 |
 |
 |
 |
 |
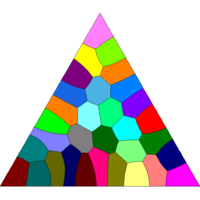 |
Tiling of a triangle with 2, 3, 4, 5, 8, 16, 24, 32 cells