Section : Tests non paramétriques
Précédent : Test de Kolmogorov-Smirnov
Suivant : Test du rapport de cotes

Test du chi-deux

Le test du chi-deux concerne uniquement les lois discrètes, mais on peut l'utiliser aussi pour des échantillons continus regroupés en classes. Le modèle de base est toujours un échantillon $ (X_1,\ldots,X_n)$ d'une loi inconnue. Les classes, notées $ c_1,\ldots,c_r$ sont une partition de l'ensemble des valeurs possibles. L'hypothèse à tester porte sur les probabilités des classes, pour lesquelles on se donne des valeurs théoriques $ P_0(c_1)\ldots,P_0(c_r)$.

$\displaystyle {\cal H}_0\;:\; \mathbb{P}[ X_i\in c_k] = P_0(c_k)\,,\;\forall k=1,\ldots,r\;. $

Sous l'hypothèse $ {\cal H}_0$, la distribution empirique de l'échantillon sur les classes doit être proche de la distribution théorique. La distribution empirique est celle des fréquences de l'échantillon dans les classes.

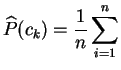$\displaystyle \widehat{P}(c_k) = \frac{1}{n}\sum_{i=1}^n$   1$\displaystyle _{c_k}(X_i)\;. $

On mesure l'adéquation de la distribution empirique à la distribution théorique par la distance du chi-deux.

Définition 2.3   On appelle distance du chi-deux de $ \widehat{P}$ par rapport à $ P_0$, et on note $ D_{\chi^2}(P_0,\widehat{P})$, la quantité :

$\displaystyle D_{\chi^2}(P_0,\widehat{P}) = \sum_{h=1}^r \frac{(P_0(c_h)-\widehat{P}(c_h))^2}{P_0(c_h)}\;. $

La ``distance'' du chi-deux est donc une moyenne pondérée d'écarts quadratiques entre les valeurs de $ P_0$ et $ \widehat{P}$. Ce n'est pas une distance au sens usuel du terme, puisqu'elle n'est même pas symétrique.

La loi de probabilité de $ D_{\chi^2}(P_0,\widehat{P})$ n'a pas d'expression explicite en général. On utilise le résultat suivant.

Théorème 2.4   Sous l'hypothèse $ {\cal H}_0$, la loi de la variable aléatoire $ nD_{\chi^2}(P_0,\widehat{P})$ converge quand $ n$ tend vers l'infini vers la loi du chi-deux de paramètre $ r\!-\!1$.

Si l'hypothèse $ {\cal H}_0$ est fausse, alors la variable $ nD_{\chi^2}(P_0,\widehat{P})$ tend vers l'infini. C'est donc un test unilatéral à droite que l'on appliquera (rejet des trop grandes valeurs).


L'exemple classique d'application du test est l'expérience de Mendel. Chez les pois, le caractère couleur est codé par un gène présentant deux formes allèles C et c, correspondant aux couleurs jaune et vert. Le jaune est dominant, le vert récessif. La forme, rond ou ridé, est portée par un autre gène à deux allèles R (dominant) et r (récessif). Si on croise deux individus dont le génotype est CcRr, on peut obtenir 16 génotypes équiprobables. Les descendants seront jaunes et ronds dans 9 cas sur 16, jaunes et ridés dans 3 cas sur 16, verts et ronds dans 3 cas sur 16, verts et ridés dans 1 cas sur 16. Dans ses expériences, Mendel a obtenu les résultats suivants.

 
Jaune
Jaune
Vert
Vert
 
Rond
Ridé
Rond
Ridé
Effectif
315
101
108
32
$ \widehat{P}(c_h)$
0.567
0.182
0.194
0.058
$ P_0(c_h)$
9/16
3/16
3/16
1/16

La valeur prise par la statistique $ nD_{\chi^2}(P_0,\widehat{P})$ est 0.47. D'après le théorème 2.4, la région de rejet doit être calculée par référence à la loi du chi-deux $ {\cal X}^2(3)$. Par exemple, au seuil 0.05, on devrait rejeter les valeurs supérieures à $ Q_{{\cal X}^2(3)}(0.95) =$ 7.81. La p-valeur de 0.47 est $ 1-F_{{\cal X}^2(3)}(0.47) =$ 0.925. Le résultat est donc tout à fait compatible avec $ {\cal H}_0$, et même un peu trop : nombreux sont ceux qui pensent que Mendel a pu arranger les résultats pour qu'ils coïncident aussi bien avec sa théorie !


L'exemple suivant concerne 10000 familles de 4 enfants pour lesquelles on connaît le nombre de garçons, entre 0 et 4. Le modèle le plus simple qu'on puisse proposer est que les naissances sont indépendantes, les deux sexes étant équiprobables. L'hypothèse nulle est donc que la loi du nombre de garçons pour une famille de 4 enfants suit la loi binomiale $ {\cal B}(4,0.5)$. Les fréquences observées et théoriques sont les suivantes :

Garçons
0
1
2
3
4
$ \widehat{P}(c_h)$
0.0572
0.2329
0.3758
0.2632
0.0709
$ P_0(c_h)$
1/16
4/16
6/16
4/16
1/16

La valeur prise par la statistique $ nD_{\chi^2}(P_0,\widehat{P})$ est 34.47. D'après le théorème 2.4, la région de rejet doit être calculée par référence à la loi du chi-deux de paramètre 5-1=4. Par exemple, au seuil 0.05, on devrait rejeter les valeurs supérieures à $ Q_{{\cal X}^2(4)}(0.95) = 9.49$. La p-valeur de 34.47 est $ 1-F_{{\cal X}^2(4)}(0.47) = 5.97\,10^{-7}$. On peut donc rejeter l'hypothèse $ {\cal H}_0$.


Le théorème 2.4 n'est qu'un résultat asymptotique. On ne peut l'utiliser que pour des tailles d'échantillons au moins de l'ordre de la centaine. De plus l'approximation qu'il décrit est d'autant moins bonne que les probabilités des classes sont faibles. Comme règle empirique, on impose parfois que l'effectif théorique $ nP(c_k)$ de chaque classe soit au moins égal à 5. Pour atteindre cet objectif, on peut être amené à effectuer des regroupements de classes, consistant à former une nouvelle classe par la réunion de plusieurs anciennes. Les fréquences empiriques et les probabilités théoriques s'ajoutent alors.


Le test du chi-deux est souvent utilisé pour tester l'ajustement à une famille particulière dépendant d'un paramètre. Dans ce cas, on est amené à estimer le paramètre à partir des données. Le théorème 2.4 n'est alors plus tout à fait valable. Si on a estimé $ h$ paramètres par la méthode du maximum de vraisemblance, à partir des fréquences des différentes classes, on doit remplacer la loi $ {\cal X}^2(r\!-\!1)$ par la loi $ {\cal X}^2(r\!-\!1\!-\!h)$.

Reprenons l'exemple du nombre de garçons dans les familles de 4 enfants, mais pour tester cette fois-ci l'hypothèse nulle :

$\displaystyle {\cal H}_0\;:\;$ le nombre de garçons suit une loi binomiale $\displaystyle {\cal B}(4,p)\;. $

Le paramètre $ p$ est inconnu et doit être estimé. L'estimateur du maximum de vraisemblance (qui maximise la probabilité des données observées) est ici le nombre total de garçons parmi les 40000 enfants. On trouve :

$\displaystyle \widehat{p} = 0.5144\;. $

On applique alors le test, mais avec une distribution théorique calculée en tenant compte de la valeur estimée du paramètre : la loi $ {\cal B}(4,\widehat{p})$.

Garçons
0
1
2
3
4
$ \widehat{P}(c_h)$
0.0572
0.2329
0.3758
0.2632
0.0709
$ P_0(c_h)$
0.0556
0.2356
0.3744
0.2644
0.0700

La valeur prise par la statistique $ nD_{\chi^2}(P_0,\widehat{P})$ est maintenant 0.9883. Elle doit être comparée aux valeurs de la loi du chi-deux de paramètre 5-1-1=3. La p-valeur de 0.9883 est $ 1-F_{{\cal X}^2(3)}(0.9883) = 0.8041$, ce qui montre que le résultat est tout à fait compatible avec l'hypothèse $ {\cal H}_0$. En conclusion, on peut accepter l'idée que les naissances sont indépendantes, mais la proportion de garçons est significativement supérieure à 0.5.


On est souvent amené à estimer des paramètres à partir des données non groupées, ou par une autre méthode que le maximum de vraisemblance. Dans ce cas, on ne dispose pas de résultat théorique clair. La valeur limite à partir de laquelle on devra rejeter l'hypothèse $ {\cal H}_0$ au seuil $ \alpha$ est comprise entre $ Q_{{\cal X}^2(r-1-h)}(1-\alpha)$ et $ Q_{{\cal X}^2(r-1)}(1-\alpha)$. En pratique, après avoir calculé la valeur $ t$ prise par $ nD_{\chi^2}(P_0,\widehat{P})$ en tenant compte de $ h$ paramètres estimés, une attitude prudente consistera à :

$ \bullet$
rejeter $ {\cal H}_0$ si $ t>Q_{{\cal X}^2(r-1)}(1-\alpha)$,
$ \bullet$
ne pas rejeter $ {\cal H}_0$ si $ t<Q_{{\cal X}^2(r-1-h)}(1-\alpha)$,
$ \bullet$
ne pas conclure si $ Q_{{\cal X}^2(r-1-h)}(1-\alpha)<t<Q_{{\cal X}^2(r-1)}(1-\alpha)$.


Un cas particulier du test du chi-deux permet de tester l'indépendance de deux caractères statistiques. Il porte le nom de chi-deux de contingence. Les deux caractères, mesurés sur une même population, sont $ X$ et $ Y$, la taille de l'échantillon est $ n$. Les modalités ou classes de $ X$ seront notées $ c_1,\ldots,c_r$, celles de $ Y$ sont notées $ d_1,\ldots,d_s$. On note :

$ \bullet$
$ n_{hk}$ l'effectif conjoint de $ c_h$ et $ d_k$ : c'est le nombre d'individus pour lesquels $ X$ prend la valeur $ c_h$ et $ Y$ la valeur $ d_k$,
$ \bullet$
$ n_{h\bullet}=\sum_{k=1}^s n_{hk}$ l'effectif marginal de $ c_h$ : c'est le nombre d'individus pour lesquels $ X$ prend la valeur $ c_h$,
$ \bullet$
$ n_{\bullet k}=\sum_{h=1}^r n_{hk}$ l'effectif marginal de $ d_k$ : c'est le nombre d'individus pour lesquels $ Y$ prend la valeur $ d_k$.
On représente ces valeurs dans un tableau à double entrée, dit tableau de contingence.

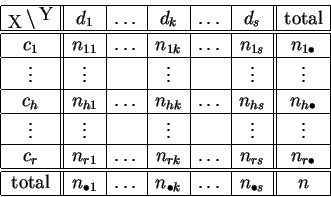
\begin{displaymath} \begin{array}{\vert c\vert\vert c\vert c\vert c\vert c\vert ... ...ots&n_{\bullet k}&\ldots&n_{\bullet s}&n\\ \hline \end{array}\end{displaymath}

Chaque ligne et chaque colonne correspond à un sous-échantillon particulier. La ligne d'indice $ h$ est la répartition sur $ d_1,\ldots,d_s$ des individus pour lesquels le caractère $ X$ prend la valeur $ c_h$. La colonne d'indice $ k$ est la répartition sur $ c_1,\ldots,c_r$ des individus pour lesquels le caractère $ Y$ prend la valeur $ d_k$. En divisant les lignes et les colonnes par leurs sommes, on obtient sur chacune des distributions empiriques constituées de fréquences conditionnelles. Pour $ h=1,\ldots,r$ et $ k=1,\ldots,s$, on les notera :

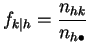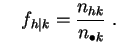
$\displaystyle f_{k\vert h} = \frac{n_{hk}}{ n_{h\bullet}}$   et$\displaystyle \quad f_{h\vert k} = \frac{n_{hk}}{ n_{\bullet k}}\;. $

Ces distributions empiriques conditionnelles s'appellent les profils-lignes et profils-colonnes.

Pour le modèle probabiliste, les observations proviennent d'un échantillon
$ ((X_1,Y_1),\ldots,(X_n,Y_n))$ d'une loi bidimensionnelle. L'hypothèse à tester est que les deux marginales de cette loi sont indépendantes. Si c'est le cas, les profils-lignes seront tous peu différents de la distribution empirique de $ Y$, et les profils-colonnes de celle de $ X$ :

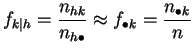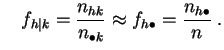
$\displaystyle f_{k\vert h} = \frac{n_{hk}}{n_{h\bullet}}\approx f_{\bullet k} = \frac{n_{\bullet k}}{ n}$   et$\displaystyle \quad f_{h\vert k} = \frac{n_{hk}}{n_{\bullet k}}\approx f_{h\bullet} = \frac{n_{h\bullet}}{n}\;. $

C'est équivalent à dire que les fréquences conjointes doivent être proches des produits de fréquences marginales.

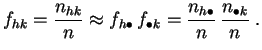
$\displaystyle f_{hk} = \frac{n_{hk}}{n} \approx f_{h\bullet}\, f_{\bullet k} =\frac{n_{h\bullet}}{n}\,\frac{n_{\bullet k}}{n}\;. $

Les fréquences conjointes d'une part (distribution observée), et les produits de fréquences marginales d'autre part (distribution théorique), constituent deux distributions de probabilité sur l'ensemble produit $ \{c_1,\ldots,c_r\}\times\{d_1,\ldots,d_s\}$. On peut donc calculer la distance du chi-deux de l'une par rapport à l'autre.

Proposition 2.5   La distance du chi-deux de contingence de la distribution empirique $ (f_{hk})$ à la distribution théorique $ (f_{h\bullet}f_{\bullet k})$ vaut :

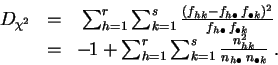
\begin{displaymath}\begin{array}{ccc} D_{\chi^2} &=& \sum_{h=1}^r\sum_{k=1}^s \f... ...^s \frac{n_{hk}^2}{n_{h\bullet}\, n_{\bullet k}}\;. \end{array}\end{displaymath}

Démonstration : La première expression est l'application directe de la définition 2.3. Pour passer à la seconde, on développe le carré.

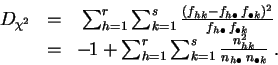
\begin{displaymath}\begin{array}{ccc} D_{\chi^2} &=& \sum_{h=1}^r\sum_{k=1}^s \f... ...^s \frac{n_{hk}^2}{n_{h\bullet}\, n_{\bullet k}}\;. \end{array}\end{displaymath}

$ \square$

D'après ce qui a été dit précédemment, pour $ n$ assez grand, on peut approcher la loi de $ nD_{\chi^2}$ par une loi du chi-deux, dont le paramètre est le nombre de classes moins 1, diminué du nombre de paramètres estimés à partir des données groupées en classes. Ici, ce sont les fréquences marginales qui ont été estimées. Il y en a $ r\!-\!1$ pour le caractère $ X$, et $ s\!-\!1$ pour le caractère $ Y$ (la dernière est le complément à 1 de la somme des autres). Le paramètre de la loi du chi-deux sera donc :

$\displaystyle rs-1-(r-1)-(s-1) = (r-1)(s-1)\;. $

Voici un exemple de deux caractères binaires, concernant des malades, pour lesquels on a observé s'il ont ou non une tendance suicidaire (caractère $ X$). Leurs maladies ont été classées en ``psychoses'' et ``névroses'' (caractère Y). On souhaite savoir s'il y a une dépendance entre les tendances suicidaires et le classement des malades. Supposons que la table de contingence observée soit :

 
tendance
sans tendance
total
psychoses
20
180
200
névroses
60
140
200
total
80
320
400

La distance du chi-deux de contingence, calculée à partir de cette table est 0.0708. La valeur prise par la statistique $ nD_{{\cal X}^2}$ est 28.33, que l'on doit comparer à la loi $ {\cal X}^2(1)$. La p-valeur est de :

$\displaystyle 1- F_{{\cal X}^2(1)}(28.33) = 1.021\,10^{-7}\;. $

On rejette donc l'hypothèse nulle, et on conclut qu'il y a une dépendance entre la tendance suicidaire et la classification des maladies.


Section : Tests non paramétriques
Précédent : Test de Kolmogorov-Smirnov
Suivant : Test du rapport de cotes