Dans de nombreuses situations, on cherche à expliquer des différences observées sur un caractère statistique, en les attribuant à l'effet d'autres caractères mesurés sur les mêmes individus. Dans l'analyse de variance, les caractères explicatifs (facteurs) ne pouvaient prendre qu'un nombre fini de modalités. Les modèles de régression sont surtout adaptés aux cas où les caractères explicatifs sont continus.
La
modélisation
probabiliste considère
que la mesure (à expliquer) effectuée sur un
individu
donné
est une
variable aléatoire,
dont la loi dépend des valeurs prises
sur cet
individu
par les
caractères
explicatifs, considérés comme
déterministes. Si ![]() désigne la
variable aléatoire
associée
à
l'individu
désigne la
variable aléatoire
associée
à
l'individu
![]() , et
, et
![]() les valeurs
prises pour cet
individu
par les
caractères
explicatifs
les valeurs
prises pour cet
individu
par les
caractères
explicatifs
![]() , on séparera l'effet déterministe et l'effet
aléatoire
par un
modèle
du type :
, on séparera l'effet déterministe et l'effet
aléatoire
par un
modèle
du type :
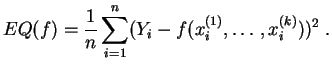
Dans certains cas classiques, on sait résoudre explicitement ce problème de minimisation, et la solution est implémentée dans les environnements de calculs statistiques. Quand une résolution explicite est impossible, on a recours à des algorithmes de minimisation, comme l'algorithme du gradient.
Nous considérons seulement la régression linéaire simple :
où
![]() est un
échantillon
de la
loi normale
est un
échantillon
de la
loi normale
![]() .
En d'autres termes, on suppose que les
.
En d'autres termes, on suppose que les ![]() sont des
variables aléatoires
gaussiennes
indépendantes,
d'espérances
sont des
variables aléatoires
gaussiennes
indépendantes,
d'espérances ![]() distinctes,
mais de même
variance
distinctes,
mais de même
variance
![]() .
Le
modèle
comporte 3 paramètres inconnus,
.
Le
modèle
comporte 3 paramètres inconnus, ![]() ,
, ![]() , et
, et ![]() .
.
Les valeurs de ![]() et
et ![]() qui minimisent l'erreur quadratique
s'expriment en fonction des
moyennes,
variances
et
covariances
empiriques de
qui minimisent l'erreur quadratique
s'expriment en fonction des
moyennes,
variances
et
covariances
empiriques de
![]() et de
et de ![]() . Nous notons :
. Nous notons :
On estime ![]() et
et ![]() en minimisant
l'erreur quadratique
:
en minimisant
l'erreur quadratique
:
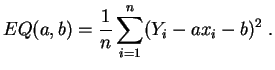
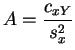 et
etL'erreur quadratique minimale est :
Ces trois
variables aléatoires
sont des
estimateurs convergents
de ![]() ,
, ![]() et
et ![]() respectivement. On obtient un
estimateur sans biais
et
convergent de
respectivement. On obtient un
estimateur sans biais
et
convergent de ![]() en posant :
en posant :
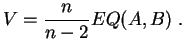
Le résultat suivant permet de calculer les lois de ces estimateurs, et donc d'en déduire des tests sur les valeurs des paramètres. On peut le considérer comme une extension du théorème 3.1.
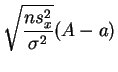 suit la
loi normale
suit la
loi normale
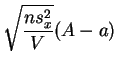 suit la
loi de Student
suit la
loi de Student
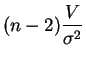 suit la
loi du chi-deux
suit la
loi du chi-deux
La première
hypothèse
que l'on souhaitera tester est que le
caractère
explicatif n'apporte pas d'information,
c'est-à-dire que la pente ![]() de la droite de régression linéaire
est nulle :
de la droite de régression linéaire
est nulle :
Selon que ![]() est supposé connu ou inconnu, on utilisera le point
1) ou le point 2) du théorème. Supposons par exemple
que
est supposé connu ou inconnu, on utilisera le point
1) ou le point 2) du théorème. Supposons par exemple
que ![]() soit inconnu, la
statistique de test
est :
soit inconnu, la
statistique de test
est :
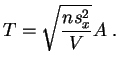
Pour le
test bilatéral
de
seuil
![]() , la
règle de décision
est :
, la
règle de décision
est :
Ce test est évidemment très proche du test de corrélation, même si les hypothèses de modélisation sont différentes.