Sección : Experimentos aleatorios
Previo : Eventos
Siguiente : Probabilidades condicionales

Axiomas de las probabilidades

Una ley de probabilidad , o distribución de probabilidad, es una función $\mathbb {P}$ que a un evento $A$ asocia un número $\mathbb {P}[A]$, su probabilidad. Este número traduce la oportunidad que tiene el evento de producirse. La forma más intuitiva de definir una tal función es repetir el experimento aleatorio y asociar a cada evento su frecuencia experimental. . Si $n$ es el número de experimentos, $n_A$ el número de veces que se produce el evento $A$, la frecuencia experimental de $A$ es la razón $n_A/n$. Aquí tenemos, como ejemplo, $20$ repeticiones de un experimento cuyas eventualidades son 0, $1$ y $2$.

$$0\,,\; 1\,,\; 1\,,\; 1\,,\; 0\,,\; 0\,,\; 1\,,\; 2\,,\; 1\,,\; 2\,,\; 0 \,,\; 1\,,\; 1\,,\; 2\,,\; 2\,,\; 0\,,\; 0\,,\; 0\,,\; 0\,,\; 2\;.$$

En este ejemplo la frecuencia experimental de $\{0\}$ es $8/20$, la de $\{1,2\}$ es $12/20$. El inconveniente es que la frecuencia experimental cambiará si rehacemos los $n$ experimentos. En otras palabras el conjunto de las $n$ repeticiones constituye un nuevo experimento aleatorio. Sin embargo todos tenemos en nuestra mente una idea de la Ley de los Grandes Números según la cual las frecuencias experimentales varían poco cuando el número de repeticiones es grande. Veamos cuatro cálculos sucesivos de la frecuencia experimental de $\{0\}$, en $20~000$ repeticiones del mismo experimento anterior.

$$0.3304\,,\;0.3273\,,\;0.3364\,,\;0.32415\;.$$

Las propiedades que esperamos de una ley de probabilidad son las mismas que las de las frecuencias experimentales. Las consideraremos como los axiomas de la definición.

A1

Para todo evento $A$, $0\leq \mathbb {P}[A]\leq 1$.

A2

La probabilidad del evento cierto es $1$: $\mathbb {P}[\Omega ]=1$.

A3

Si $(A_i)_{i\in\mathbb {N}}$ es una sucesión de eventos disjuntos dos a dos ($A_i$ y $A_j$ no pueden suceder a la vez si $i\neq j$), entonces:

$$\mathbb {P}[\bigcup\limits_{i\in\mathbb {N}}A_i] =\sum\limits_{i\in\mathbb {N}}\mathbb {P}[A_i] \;.$$

Una consecuencia inmediata de los axiomas A2 y A3 es la relación entre la probabilidad de un evento $A$ y la de su opuesto, denotado $\overline A$.

$$\mathbb {P}[\overline A] = 1 - \mathbb {P}[A] \;.$$

Una ley de probabilidad es creciente por inclusión, según A1 y A3: si $A\subset B$, entonces $\mathbb {P}[A]\leq \mathbb {P}[B]$.

Las leyes de probabilidad que se emplean en la práctica son de dos tipos particulares, las leyes discretas y las leyes continuas.

1. Leyes discretas
El conjunto de las eventualidades $\Omega$ es finito o numerable:

$$\Omega = \{ \omega_i\,,\;i\in I\subset \mathbb {N}\}\;.$$

Todas las partes de $\Omega$ son eventos. Como todo evento es una reunión finita o numerable de eventos individuales o aislados (singleton), es suficiente definir la probabilidad de cada singleton:

$$\forall \omega_i\in \Omega\;,\quad \mathbb {P}[\{\omega_i\}] = p_i\;.$$

Para todo $A\subset \Omega$, la probabilidad de $A$ será entonces determinada por A3:

$$\mathbb {P}[A] = \sum_{\omega_i\in A} \mathbb {P}[\{\omega_i\}] = \sum_{\omega_i\in A} p_i\;.$$

Ejemplo: Si el conjunto de los resultados es finito $\Omega =\{\omega _1, \ldots ,\omega _n\}$ y si no hay información que nos permita diferenciar unos resultados de otros, es natural asociar a cada eventualidad la probabilidad $1/n$. La probabilidad de todo evento $A$ es entonces Card$(A)/n$.

Esta probabilidad particular se llama la equiprobabilidad. En este caso todos los cálculos se convierten en contar:

   probabilidad$$=\frac{\mbox{n\'umero de casos favorables} }{\mbox{n\'umero total de casos}}\;.$$

2. Leyes continuas

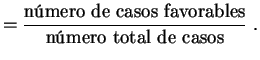
El conjunto de las eventualidades $\Omega$ es $\mathbb {R}$. Los eventos son los intervalos, y todos los subconjuntos de $\mathbb {R}$ que se pueden formar combinando intersecciones y uniones de intervalos. En la teoría de la medida se les llama conjuntos borelianos.

Definición 1.1   Llamamos densidad de probabilidad a una función de $\mathbb {R}$ en $\mathbb {R}^+$, continua por pedazos y de integral igual a $1$.

$$f(x)\geq 0\;,\;\forall x\in \mathbb {R}$$   y$$\quad \int_{\mathbb {R}} f(x)\,dx = 1\;.$$

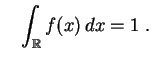
Dada una densidad de probabilidad, se define una ley de probabilidad sobre $\mathbb {R}$, asociando a todo evento $A$ el valor de la integral de la densidad sobre este evento:

$$\mathbb {P}[A] = \int_{A} f(x)\,dx\;.$$

Ejemplo: Para el experimento aleatorio que consiste en sacar al azar un número real en el intervalo $[0,1]$ (llamar a Random ), consideraremos sobre $\mathbb {R}$ la ley de probabilidad continua de densidad:

$$f(x) = \left\{ \begin{array}{ll} 1&\mbox{si } x\in [0 ,1]\;,\\ 0&\mbox{si no.}\\ \end{array} \right.$$

Ella asigna a todo intervalo contenido en $[0,1]$ una probabilidad igual a su longitud.

Como sucede en el ejemplo anterior, es frecuente que una densidad sea estrictamente positiva sobre un intervalo (eventualmente no acotado) de $\mathbb {R}$, y nula fuera. El intervalo en el cual $f$ es estrictamente positiva se llama el soporte de la ley.

Podemos ver una probabilidad como una distribución de masa en el conjunto de las eventualidades. La masa total vale $1$. En el caso discreto, ella se encuentra repartida en cada eventualidad como en ``granos de plomo'' separados. En el caso continuo, ella está repartida sobre todo un intervalo de $\mathbb {R}$, que es como un hilo de masa $1$ en el cual la densidad de la masa es variable. Calcular la probabilidad de un evento es calcular su masa. Aparte de esta analogía, ¿qué sentido práctico tiene la noción de probabilidad? ¿Podemos medir físicamente probabilidades?

El único sentido concreto que les podemos dar es, intuitivamente, el de la Ley de los Grandes Números. ``Cara tiene una posibilidad sobre dos de suceder'' significa para nosotros que ``si lanzo la moneda una gran cantidad de veces, Cara saldrá alrededor de una vez de cada dos.''

Intuición: La probabilidad de un evento es el límite de sus frecuencias experimentales en un gran número de experimentos independientes.

Esta idea intuitiva conlleva varios puntos oscuros. Que las frecuencias experimentales convergen bajo ciertas hipótesis es un teorema (este teorema es el que lleva el nombre de Ley de los Grandes Números). ¿Por qué añadir el adjetivo ``independientes''?

Imaginemos una máquina de precisión para lanzar monedas: un brazo articulado dotado de un plato, unido a un muelle regulable, ajustado a un valor fijo. Pongamos el muelle en tensión y depositemos una moneda en el plato, con la Cara hacia arriba y soltemos el muelle. La primera vez no podremos prever si la moneda caerá de Cara o Cruz, pero la información que obtenemos en el resultado del primer ensayo permitirá predecir los siguientes: los experimentos no son independientes. Las frecuencias experimentales valdrán $1$ ó 0 pero no brindarán ninguna información sobre si la moneda está adulterada o no.

El objetivo principal del próximo parrafo es precisar las nociones de dependencia e independenciaide eventos y de experimentos aleatorios.

Sección : Experimentos aleatorios
Previo : Eventos
Siguiente : Probabilidades condicionales